题目内容
3．设Sn为等差数列{an}的前项和，若S3=3，S6=24，则a9=（ ）| A． | 15 | B． | 45 | C． | 192 | D． | 27 |
分析 设等差数列{an}的首项是a1、公差是d，由题意和等差数列的前n项和公式列出方程组，求出a1、d的值，由等差数列的通项公式求出a9的值．
解答 解：设等差数列{an}的首项是a1、公差是d，
因为S3=3，S6=24，
所以$\left\{\begin{array}{l}{3{a}_{1}+3d=3}\\{6{a}_{1}+15d=24}\end{array}\right.$，解得$\left\{\begin{array}{l}{{a}_{1}=-1}\\{d=2}\end{array}\right.$，
则a9=-1+8×2=15，
故选：A．
点评 本题考查等差数列的前n项和公式，以及通项公式，考查方程思想和计算能力，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
13．设M={2}，N={2，3}，则下列表示不正确的是（ ）
| A． | M?N | B． | M⊆N | C． | 2∈N | D． | 2?N |
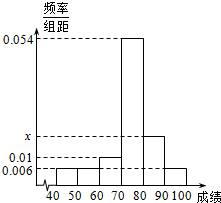某班50位学生2015届中考试数学成绩的频率直方分布图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．
15．已知复数$\frac{2a+i}{2i-1}$是纯虚数，则实数a=（ ）
| A． | -1 | B． | -$\frac{1}{4}$ | C． | $\frac{1}{4}$ | D． | 1 |