题目内容
14．设函数y=f（x）的图象与y=2x+a的图象关于直线y=x对称，且f（2）+f（4）=1，则a=（ ）| A． | -1 | B． | 1 | C． | 2 | D． | 4 |
分析 由已知可得函数y=f（x）与y=2x+a互为反函数，求出函数f（x）的解析式，结合f（2）+f（4）=1，可得答案．
解答 解：∵函数y=f（x）的图象与y=2x+a的图象关于直线y=x对称，
故函数y=f（x）与y=2x+a互为反函数，
则f（x）=log2x-a，
又∵f（2）+f（4）=1-a+2-a=1，
∴a=1，
故选：B．
点评 本题考查的知识点是反函数，根据函数y=f（x）与y=2x+a互为反函数，求出函数f（x）的解析式，是解答的关键．
练习册系列答案
相关题目
4．
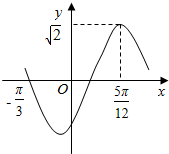函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）
函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）| A． | $[\frac{5π}{12}+kπ，\frac{11π}{12}+kπ]，k∈z$ | B． | $[\frac{5π}{6}+kπ≤x≤\frac{11π}{6}+kπ]，k∈z$ | ||
| C． | $[\frac{5π}{12}+2kπ，\frac{11π}{12}+2kπ]，k∈z$ | D． | $[-\frac{π}{12}+kπ，\frac{5π}{12}+kπ]，k∈z$ |
19．点P（1，-2）关于点M（3，0）的对称点Q的坐标是（ ）
| A． | （1，2） | B． | （2，-1） | C． | （3，-1） | D． | （5，2） |
3．设Sn为等差数列{an}的前项和，若S3=3，S6=24，则a9=（ ）
| A． | 15 | B． | 45 | C． | 192 | D． | 27 |