题目内容
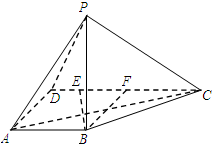
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,AB∥CD,AD⊥AB,AB=2,AD=
如图,四棱锥P-ABCD中,PB⊥底面ABCD,AB∥CD,AD⊥AB,AB=2,AD=| 2 |
(1)证明:BE⊥平面PBC;
(2)求三棱锥B-PAC的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)由公演股定理得BE⊥BC,由线面垂直得PB⊥BE,由此能证明BE⊥平面PBC.
(2)由VB-PAC=VP-ABC,利用等积法能求出三棱锥B-PAC的体积.
(2)由VB-PAC=VP-ABC,利用等积法能求出三棱锥B-PAC的体积.
解答:
 (本小题满分14分)
(本小题满分14分)
(1)证明:过B作CD的垂线交CD于F,则BF=AD=
,EF=AB-DE=1,FC=2
在Rt△BFE中,BE=
=
,
在Rt△BFC中,BD=
=
.
在△BCE中,∵BE2+BC2=BC2,∴BE⊥BC,
∵PB⊥底面ABCD,BE?平面ABCD,∴PB⊥BE,
又PB∩BC=B∴BE⊥平面PBC.…(8分)
(2)解:∵AB∥CD,AD⊥AB,∴四边形ABCD是梯形,
∴S梯形ABCD=
×(2+4)×
=3
,S△ADC=
×4×
=2
,
∴S△ABC=S梯形ABCD-S△ADC=3
-2
=
.
∴VB-PAC=VP-ABC=
S△ABC•PB=
×
×3=
.…(14分)
 (本小题满分14分)
(本小题满分14分)(1)证明:过B作CD的垂线交CD于F,则BF=AD=
| 2 |
在Rt△BFE中,BE=
| EF2+BF2 |
| 3 |
在Rt△BFC中,BD=
| FC2+BF2 |
| 6 |
在△BCE中,∵BE2+BC2=BC2,∴BE⊥BC,
∵PB⊥底面ABCD,BE?平面ABCD,∴PB⊥BE,
又PB∩BC=B∴BE⊥平面PBC.…(8分)
(2)解:∵AB∥CD,AD⊥AB,∴四边形ABCD是梯形,
∴S梯形ABCD=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴S△ABC=S梯形ABCD-S△ADC=3
| 2 |
| 2 |
| 2 |
∴VB-PAC=VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
点评:本题考查直线与平面平行的证明,考查三棱锥体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
下面使用类比推理,得到正确结论的是( )
| A、“若a•3=b•3,则a=b”类推出“若a•0=b•0,则a=b” | ||||||
| B、“若(a+b)c=ac+bc,”类推出“(a•b)c=ac•bc” | ||||||
C、“若(a+b)c=ac+bc”类推出“
| ||||||
| D、“(ab)n=anbn”类推出“(a+b)n=an+bn” |