题目内容
1.若$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(1,-1),$\overrightarrow{c}$=(1,2).用$\overrightarrow{a},\overrightarrow{b}$表示$\overrightarrow{c}$,则$\overrightarrow{c}$=$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$.分析 利用平面向量坐标运算法则求解.
解答 解:∵$\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(1,-1),$\overrightarrow{c}$=(1,2),
设$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\left\{\begin{array}{l}{x+y=1}\\{x-y=2}\end{array}\right.$,解得x=$\frac{3}{2}$,y=-$\frac{1}{2}$,
∴$\overrightarrow{c}$=$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$.
故答案为:$\frac{3}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$.
点评 本题考查向量的坐标运算,是基础题,解题时要认真审题,注意平面向量坐标运算法则的合理运用.

练习册系列答案
相关题目
13.从一个边长为2的等边三角形的中心、各边中点及三个顶点这7个点中任取两个点,则这两点间的距离小于1的概率是( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
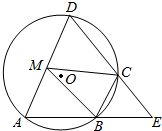 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.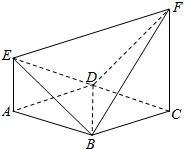 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1