题目内容
8.已知各项为正数的数列{an}的前n项和为Sn,且a1=$\frac{1}{3}$,an+1-an+4an+1an=0,n∈N*(1)求{an}的通项公式;
(2)求数列{$\frac{{2}^{n-1}}{{a}_{n}}$}的前n项和Tn.
分析 (1)化简an+1-an+4an+1an=0可得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=4,从而解得;
(2)化简$\frac{{2}^{n-1}}{{a}_{n}}$=(4n-1)2n-1,从而利用错位相减法求其前n项和.
解答 解:(1)由题意知,an>0,
∵an+1-an+4an+1an=0,
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$+4=0,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=4,
又∵$\frac{1}{{a}_{1}}$=3,
∴{$\frac{1}{{a}_{n}}$}是以3为首项,4为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=3+4(n-1)=4n-1,
∴an=$\frac{1}{4n-1}$;
(2)$\frac{{2}^{n-1}}{{a}_{n}}$=(4n-1)2n-1,
Tn=3+7•2+11•4+…+(4n-1)2n-1,
2Tn=3•2+7•4+11•8+…+(4n-1)2n,
∴两式作差可得,
Tn=-3-4(2+4+8+…+2n-1)+(4n-1)2n
=-3-4$\frac{2(1-{2}^{n-1})}{1-2}$+(4n-1)2n
=(4n-5)2n+5.
点评 本题考查了等比数列与等差数列的性质的应用及构造法的应用,同时考查了错位相减法的应用.

练习册系列答案
相关题目
16.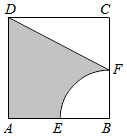 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
 如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )
如图所示,在边长为2的正方形ABCD中,圆心为B,半径为1的圆与AB、BC分别交于E,F,则阴影部分绕直线BC旋转一周形成几何体的体积等于( )| A. | π | B. | 6π | C. | $\frac{4π}{3}$ | D. | 4π |
3.用1,2,3,4四个数字组成一个四位数,其中大于3300的偶数有多少个( )
| A. | 128 | B. | 64 | C. | 96 | D. | 48 |
17.已知命题p:?x>0,sinx>-1;q:?x>0,cosx>-1,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
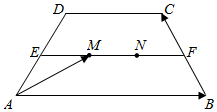 如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.
如图,已知四边形ABCD是等腰梯形,E、F分别是腰AD、BC的中点,M、N是线段EF上的两个点,且EM=MN=NF,下底是上底的2倍,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,求$\overrightarrow{AM}$.