题目内容
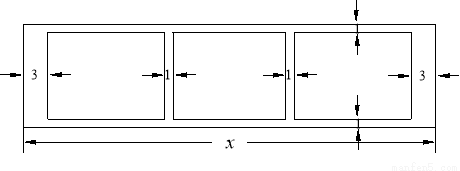
(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为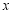 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为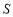 (m2).
(m2).
(1)求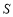 关于
关于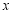 的函数关系式;
的函数关系式;
(2)求 的最大值.
的最大值.
(1)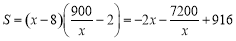 ,
,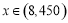 .
.
2)当矩形温室的室内长为60 m时,三块种植植物的矩形区域的总面积最大,最大为 m2 .
m2 .
【解析】
试题分析:(1)建立实际问题函数解析式,关键读懂题意即可,本题题意明确,图形简单,三块种植植物的矩形区域的总面积可看做一个矩形面积: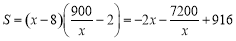 ,根据边长为正得其定义域为
,根据边长为正得其定义域为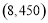
(2)这是一个积为定值的函数,可根据基本不等式求最值: 当且仅当
当且仅当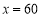 时等号成立.
时等号成立.
试题解析:(1)由题设,得
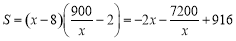 ,
,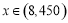 . 6分
. 6分
(2)因为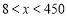 ,所以
,所以 , 8分
, 8分
当且仅当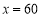 时等号成立. 10分
时等号成立. 10分
从而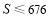 . 12分
. 12分
答:当矩形温室的室内长为60 m时,三块种植植物的矩形区域的总面积最大,最大为 m2 . 14分
m2 . 14分
考点:函数解析式,基本不等式求最值
考点分析: 考点1:函数模型及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 B=
B=
 的方差为
的方差为 ,则
,则 .
. 的定义域是
的定义域是 ,则实数
,则实数 的值为 .
的值为 . 为虚数单位
为虚数单位 ,则
,则 .
.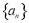 的公比为
的公比为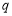 (
(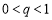 ),前n项和为
),前n项和为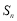 ,若
,若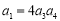 ,且
,且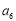 与
与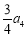 的等差中项为
的等差中项为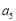 ,则
,则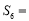 .
. 的最小正周期为 .
的最小正周期为 .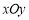 中,已知圆
中,已知圆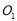 ,圆
,圆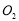 均与
均与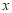 轴相切且圆心
轴相切且圆心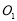 ,
,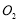 与原点
与原点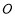 共线,
共线,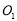 ,
,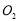 两点的横坐标之积为6,设圆
两点的横坐标之积为6,设圆 ,
,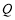 两点,直线
两点,直线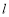 :
: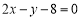 ,则点
,则点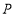 与直线
与直线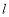 上任意一点
上任意一点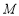 之间的距离的最小值为 .
之间的距离的最小值为 . ,
, .
. ;
; 在
在 恒成立,求
恒成立,求 的最小值.
的最小值.