题目内容
(本小题满分12分)已知函数 ,
, .
.
(1)证明: ;
;
(2)若 在
在 恒成立,求
恒成立,求 的最小值.
的最小值.
(1)详见解析;(2)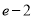 .
.
【解析】
试题分析:(1)求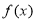 的导数,判断
的导数,判断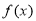 在
在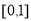 上的单调性,从而可求函数的最小值,即可证明不等式成立;(2)令
上的单调性,从而可求函数的最小值,即可证明不等式成立;(2)令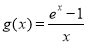 ,可知
,可知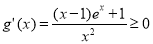 ,从而
,从而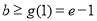 ,而
,而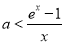 等价于
等价于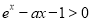 在
在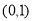 上恒成立,分类讨论,即可求得实数
上恒成立,分类讨论,即可求得实数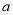 的取值范围.
的取值范围.
试题解析:(1)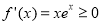 ,即
,即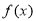 在
在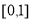 上单调递增,∴
上单调递增,∴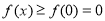 ,即结论成立; (2)令
,即结论成立; (2)令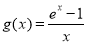 ,则
,则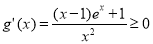 ,
,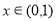 ,∴当
,∴当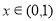 时,
时,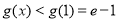 ,要使
,要使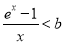 ,只需
,只需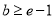 ,要使
,要使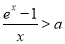 成立,只需
成立,只需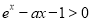 在
在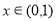 恒成立,令
恒成立,令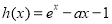 ,
,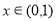 ,则
,则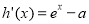 ,由
,由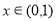 ,
,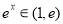 ,①当
,①当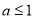 时,
时,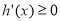 ,此时
,此时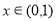 ,有
,有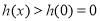 成立,∴
成立,∴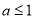 满足条件,②当
满足条件,②当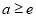 时,
时,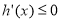 ,此时
,此时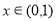 ,有
,有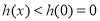 ,不符合题意,舍去,③当
,不符合题意,舍去,③当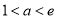 时,令
时,令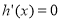 ,得
,得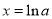 ,可得当
,可得当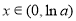 时,
时,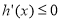 ,即
,即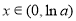 时,
时,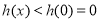 ,不符合题意,舍去,综上,
,不符合题意,舍去,综上,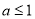 ,又∵
,又∵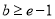 ,
,
∴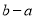 的最小值为
的最小值为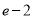 .
.
考点:1.利用导数求函数在闭区间上的最值;2.恒成立问题;3.分类讨论的数学思想.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
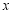 (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为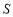 (m2).
(m2).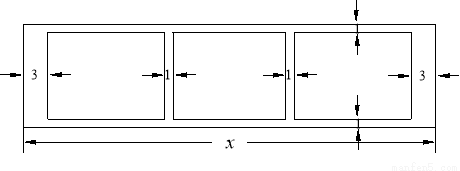
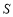 关于
关于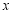 的函数关系式;
的函数关系式; 的最大值.
的最大值. (
( ,i为虚数单位),若
,i为虚数单位),若 ,则
,则 的值为 .
的值为 . ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
 满足
满足 ,
, ,则该数列的前
,则该数列的前 项的乘积
项的乘积 _________.
_________. 的图象大致是( )
的图象大致是( )
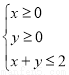 所表示的平面区域被直线
所表示的平面区域被直线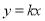 分为面积相等的两部分,则
分为面积相等的两部分,则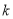 的值是 .
的值是 .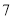 个,从袋子中任取
个,从袋子中任取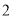 个球都是白球的概率为
个球都是白球的概率为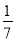 ,每个球被取到的机会均等.现从袋子中每次取
,每个球被取到的机会均等.现从袋子中每次取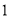 个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为
个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为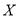 .
.