题目内容
7．已知数列{an}满足，${a_n}=2+2{cos^2}\frac{nπ}{2}$，n∈N*，等差数列{bn}满足a1=2b1，a2=b2．（1）求bn；
（2）记cn=a2n-1b2n-1+a2nb2n，求cn；
（3）求数列{anbn}前2n项的和S2n．
分析 （1）利用二倍角公式化简an，可得an=$\left\{\begin{array}{l}{2，n为奇数}\\{4，n为偶数}\end{array}\right.$．求出数列{bn}的首项和公差，则通项公式可求；
（2）直接把{an}、{bn}的通项公式代入求解；
（3）由（2）知，数列{cn}是以36为公差的等差数列，再由等差数列的前n项和公式得答案．
解答 解：（1）由${a_n}=2+2{cos^2}\frac{nπ}{2}$=2+1+cosnπ=3+cosnπ=$\left\{\begin{array}{l}{2，n为奇数}\\{4，n为偶数}\end{array}\right.$．
于是，${b}_{1}=\frac{1}{2}{a}_{1}=1$，b2=a2=4，
∴等差数列{bn}的公差为3，则bn=1+3（n-1）=3n-2；
（2）cn=a2n-1b2n-1+a2nb2n=2[3（2n-1）-2]+4[3×2n-2]=36n-18；
（3）由（2）知，数列{cn}是以36为公差的等差数列，
则S2n=a1b1+a2b2+…+a2n-1b2n-1+a2nb2n
=$\frac{n（{c}_{1}+{c}_{n}）}{2}$=$\frac{n（18+36n-18）}{2}=18{n}^{2}$．
点评 本题考查数列递推式，考查了等差关系的确定，训练了等差数列前n项和的求法，是中档题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
18．命题“?x＞0，lnx≤x-1”的否定是（ ）
| A． | ?x0＞0，lnx0≤x0-1 | B． | ?x0＞0，lnx0＞x0-1 | C． | ?x0＜0，lnx0＜x0-1 | D． | ?x0＞0，lnx0≥x0-1 |
15．设复数z满足iz=1+2i，则z的共轭复数的虚部为（ ）
| A． | i | B． | -i | C． | -1 | D． | 1 |
2．
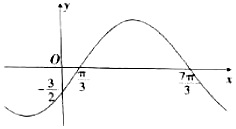已知函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，将函数y=f（x）的图象向左平移$\frac{4π}{3}$个单位，得到函数y=g（x）的图象，则函数y=g（x）在区间$[{\frac{π}{2}，\frac{5π}{2}}]$上的最大值为（ ）
已知函数$f（x）=Asin（{ωx+φ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，将函数y=f（x）的图象向左平移$\frac{4π}{3}$个单位，得到函数y=g（x）的图象，则函数y=g（x）在区间$[{\frac{π}{2}，\frac{5π}{2}}]$上的最大值为（ ）| A． | 3 | B． | $\frac{{3\sqrt{3}}}{2}$ | C． | $\frac{{3\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
12．已知集合M={1，3，4}，N={x|x2-4x+3=0}，则M∩N=（ ）
| A． | {3，4} | B． | {1，4} | C． | {1，3} | D． | {3} |
19．已知直线ax+by-8=0（a＞0，b＞0）被圆x2+y2-2x-4y=0截得的弦长为2$\sqrt{5}$，则ab的最大值是（ ）
| A． | $\frac{5}{2}$ | B． | 4 | C． | $\frac{9}{2}$ | D． | 8 |
17．设双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点分别为F1，F2，以F1F2为直径的圆与双曲线左支的一个交点为P，若以OF1（O为坐标原点）为直径的圆与PF2相切，则双曲线C的离心率为（ ）
| A． | $\sqrt{2}$ | B． | $\frac{-3+6\sqrt{2}}{4}$ | C． | $\sqrt{3}$ | D． | $\frac{3+6\sqrt{2}}{7}$ |