题目内容
19．已知直线ax+by-8=0（a＞0，b＞0）被圆x2+y2-2x-4y=0截得的弦长为2$\sqrt{5}$，则ab的最大值是（ ）| A． | $\frac{5}{2}$ | B． | 4 | C． | $\frac{9}{2}$ | D． | 8 |
分析 由圆的性质及点到直线的距离公式得圆心（1，2）在直线ax+by-8=0上，而a+2b=8，由此利用均值定理能求出ab的最大值．
解答 解：由圆x2+y2-2x-4y=0，得（x-1）2+（y-2）2=5，
∴圆心（1，2），半径r=$\sqrt{5}$，
直线ax+by-8=0（a＞0，b＞0）被圆x2+y2-2x-4y=0截得的弦长为2$\sqrt{5}$，
∴圆心（1，2）在直线ax+by-8=0上，
∴a+2b=8，
∵a＞0，b＞0，
∴2ab≤（$\frac{a+2b}{2}$）2=16，即ab≤8，
∴当且仅当a=2b=4时，ab取最大值8．
故选：D．
点评 本题考查两数积的最大值的求法，是中档题，解题时要注意圆的性质、点到直线距离公式、均值定理的合理运用．
练习册系列答案
相关题目
9．已知函数f（x）=-x2-6x-3，设max{p，q}表示p，q二者中较大的一个．函数g（x）=max{（$\frac{1}{2}$）x-2，log2（x+3）}．若m＜-2，且?x1∈[m，-2），?x2∈（0，+∞），使得f（x1）=g（x2）成立，则m的最小值为（ ）
| A． | -5 | B． | -4 | C． | -2$\sqrt{5}$ | D． | -3 |
10．
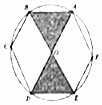已知正六边形ABCDEF内接于圆O，连接AD，BE，现在往圆O内投掷2000粒小米，则可以估计落在阴影区域内的小米的粒数大致是（ ）（参考数据：$\frac{π}{\sqrt{3}}$=1.82，$\frac{\sqrt{3}}{π}$=0.55）
已知正六边形ABCDEF内接于圆O，连接AD，BE，现在往圆O内投掷2000粒小米，则可以估计落在阴影区域内的小米的粒数大致是（ ）（参考数据：$\frac{π}{\sqrt{3}}$=1.82，$\frac{\sqrt{3}}{π}$=0.55）| A． | 550 | B． | 600 | C． | 650 | D． | 700 |
14．“x＞1“是“2x＞1”的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
8．设全集U={-2，-1，0，1，2，3}，A={2，3}，B={-1，0}，则A∩（∁UB）=（ ）
| A． | {0，2，3} | B． | {-2，1，2，3} | C． | {-1，0，2，3} | D． | {2，3} |