题目内容
17.设双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,以F1F2为直径的圆与双曲线左支的一个交点为P,若以OF1(O为坐标原点)为直径的圆与PF2相切,则双曲线C的离心率为( )| A. | $\sqrt{2}$ | B. | $\frac{-3+6\sqrt{2}}{4}$ | C. | $\sqrt{3}$ | D. | $\frac{3+6\sqrt{2}}{7}$ |
分析 设F1N=ON=MN=r,则OF2=2r,根据勾股定理NF2=2$\sqrt{2}$r,再利用相似三角形和双曲线的离心率公式即可求得
解答 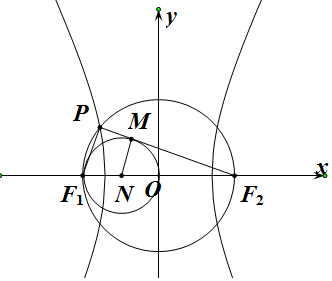 解:设F1N=ON=MN=r,
解:设F1N=ON=MN=r,
则OF2=2r,
根据勾股定理NF2=2$\sqrt{2}$r,
又△MF2N∽△PF1F2,
∴e=$\frac{c}{a}$=$\frac{2c}{2a}$=$\frac{{F}_{1}{F}_{2}}{P{F}_{2}-P{F}_{1}}$=$\frac{N{F}_{2}}{M{F}_{2}-MN}$=$\frac{3r}{2\sqrt{2}r-r}$=$\frac{6\sqrt{2}+3}{7}$,
故选:D
点评 此题要求学生掌握定义:到两个定点的距离之差等于|2a|的点所组成的图形即为双曲线.考查了数形结合思想、本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
8.设全集U={-2,-1,0,1,2,3},A={2,3},B={-1,0},则A∩(∁UB)=( )
| A. | {0,2,3} | B. | {-2,1,2,3} | C. | {-1,0,2,3} | D. | {2,3} |
12.数列1,$\frac{1}{1+2}$,$\frac{1}{1+2+3}$,…,$\frac{1}{1+2+3+…+n}$的前n项和为$\frac{9}{5}$,则正整数n的值为( )
| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
9.根据如图的程序框图,当输入x为2017时,输出的y为28,则判断框中的条件可以是( )


| A. | x≥0? | B. | x≥1? | C. | x≥-1? | D. | x≥-3? |
10.某项科研活动共进行了5次试验,其数据如表所示:
(Ⅰ)从5次特征量y的试验数据中随机地抽取两个数据,求至少有一个大于600的概率;
(Ⅱ)求特征量y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并预测当特征量x为570时特征量y的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| 特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| x | 555 | 559 | 551 | 563 | 552 |
| y | 601 | 605 | 597 | 599 | 598 |
(Ⅱ)求特征量y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;并预测当特征量x为570时特征量y的值.
(附:回归直线的斜率和截距的最小二乘法估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
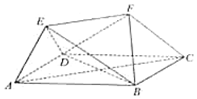 如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.
如图,在多面体ABCDEF中,底面ABCD是菱形,AB=2,∠DAB=60°,EF∥AC,EF=$\sqrt{3}$.