题目内容
7.设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-1(x>0)}\\{2-3x(x≤0)}\end{array}\right.$,f(a)<8,则实数a的取值范围(-2,2).分析 由已知条件结合分段函数的性质得当a>0时,3a-1<8,当a≤0时,2-3a<8,由此能求出实数a的取值范围.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-1(x>0)}\\{2-3x(x≤0)}\end{array}\right.$,f(a)<8,
∴当a>0时,3a-1<8,解得0<a<2,
当a≤0时,2-3a<8,解得-2<a≤0.
∴实数a的取值范围是(-2,2).
故答案为:(-2,2).
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意分段函数的性质的合理运用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
17.集合A={x|-3≤x<4}所表示的区间为( )
| A. | (-3,4) | B. | [-3,4] | C. | (-3,4] | D. | [-3,4) |
2.已知a,b∈N*,f(x)=ex-2x,则“f(a)>f(b)”是“a>b”的 ( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必娄条件 |
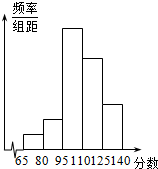 为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.
为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.