题目内容
16.若函数f(x)满足$f({x-1})=\frac{1}{f(x)-1}$,当x∈[-1,0]时,f(x)=x,若在区间[-1,1]上,g(x)=f(x)-mx+m有两个零点,则实数m的取值范围为(0,$\frac{1}{2}$].分析 根据$f({x-1})=\frac{1}{f(x)-1}$,当x∈[-1,0]时,f(x)=x,求出x∈(0,1)时,f(x)的解析式,由在区间(-1,1]上,g(x)=f(x)-mx+m有两个零点,转化为两函数图象的交点,利用图象直接的结论.
解答 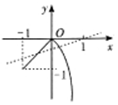 解:∵x∈(-1,0)时,f(x)=x,∴当x∈(0,1]时,x-1∈(-1,0),$f({x-1})=\frac{1}{f(x)-1}$,可得x-1=$\frac{1}{f(x)-1}$,所以f(x)=$\frac{1}{x-1}+1$,作出f(x)在[-1,1)上的图象,如图:
解:∵x∈(-1,0)时,f(x)=x,∴当x∈(0,1]时,x-1∈(-1,0),$f({x-1})=\frac{1}{f(x)-1}$,可得x-1=$\frac{1}{f(x)-1}$,所以f(x)=$\frac{1}{x-1}+1$,作出f(x)在[-1,1)上的图象,如图:
因为g(x)=f(x)-mx-m有两个零点,所以y=f(x)的图象与直线y=mx-m有两个交点,由图象可知m∈(0,$\frac{1}{2}$].
故答案为:(0,$\frac{1}{2}$].
点评 此题是个中档题.本题考查了利用函数零点的存在性求变量的取值范围和代入法求函数解析式,体现了转化的思想,以及利用函数图象解决问题的能力,体现了数形结合的思想.也考查了学生创造性分析解决问题的能力.

练习册系列答案
相关题目
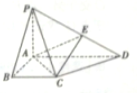 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$. 如图所示,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.
如图所示,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,$∠DAB=\frac{π}{3}$,PD⊥AD,PD⊥DC.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,$∠DAB=\frac{π}{3}$,PD⊥AD,PD⊥DC. 如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1-BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题:
如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1-BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题: