题目内容
10.设函数f(x)=$\frac{{e}^{x}}{x}$+$\frac{a}{x}$+b,g(x)=kx,曲线y=f(x)在点(1,f(1))处的切线方程为x-y+e-3=0(e为自然对数的底数)(Ⅰ)求a,b;
(Ⅱ)若x>0时,f(x)>g(x),求k的取值范围.
分析 (Ⅰ)求出f(x)的导数,求得切线的斜率和切点,由已知切线的方程,解方程可得a,b;
(Ⅱ)由题意可得x>0时,$\frac{{e}^{x}}{x}$-$\frac{1}{x}$-1>kx,即ex-1-x>kx2,由h(x)=ex-1-x,求出导数,可得ex≥1+x,由m(x)=ex-1-x-kx2,求得导数,讨论2k与1的关系,即可求得k的范围.
解答 解:(Ⅰ)f(x)=$\frac{{e}^{x}}{x}$+$\frac{a}{x}$+b的导数为f′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$-$\frac{a}{{x}^{2}}$,
在点(1,f(1))处的切线斜率为-a,切点为(1,e+a+b),
由切线方程为x-y+e-3=0,可得-a=1,e+a+b=e-2,
解得a=b=-1;
(Ⅱ)x>0时,f(x)>g(x),
即为x>0时,$\frac{{e}^{x}}{x}$-$\frac{1}{x}$-1>kx,
即ex-1-x>kx2,
由h(x)=ex-1-x的导数为h′(x)=ex-1,
当x>0时,h′(x)>0,h(x)递增;当x<0时,h′(x)<0,h(x)递减.
可得h(x)在x=0处取得最小值0,即有h(x)≥0成立,
即ex≥1+x,
ex-1-x-kx2>0在x>0恒成立,
由m(x)=ex-1-x-kx2,m′(x)=ex-1-2kx,
当2k≤1时,由ex≥1+x,可得ex-1-2kx≥ex-1-x>0,
则m(x)在x>0时递增,即有m(x)>m(0)=0,
即有ex-1-x-kx2>0在x>0恒成立;
当2k>1时,ex-1-x-kx2>0在x>0不恒成立.
综上可得,k的范围是(-∞,$\frac{1}{2}$].
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查不等式恒成立问题的解法,注意运用构造函数,由导数判断单调性,属于中档题.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案| 广告支出x(单位:万元) | 1 | 2 | 3 | 4 |
| 销售收入y(单位:万元) | 12 | 28 | 42 | 56 |
(2)若广告费为9万元,则销售收入为多少万元?
(参考公式:$b=\frac{{{x_1}{y_1}+{x_2}{y_2}+…+{x_n}{y_n}-n\overline x•\overline y}}{{x_1^2+x_2^2+…+x_n^2-n{{\overline x}^2}}}$,$a=\overline y-b\overline x$)
| A. | 出租车车费与形式里程 | B. | 房屋面积与房屋价格 | ||
| C. | 身高与体重 | D. | 铁块的体积与质量 |
| A. | f(x)<g(x)<h(x) | B. | g(x)<f(x)<h(x) | C. | g(x)<h(x)<f(x) | D. | h(x)<g(x)<f(x) |
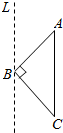 如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.
如图,等腰直角三角形ABC,|AB|=$\sqrt{2}$,AC∥L,三角形ABC绕直线L旋转一周,得到的几何体的体积为$\frac{4π}{3}$.