题目内容
3.给出计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2018}$的值的一个程序框图如图,其中判断框内应填入的条件是( )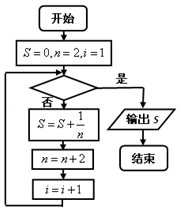
| A. | i>1009? | B. | i<1009? | C. | i>2018? | D. | i<2018? |
分析 由题意可知,首先是判断框中的条件不满足,所以框图依次执行循环,框图执行第一次循环后,S的值为1,执行第二次循环后,S的值为前2项的和,满足S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2018}$,此时i的值为1010,判断框中的条件应该满足,算法结束,由此得到判断框中的条件.
解答 解:框图首先给累加变量S赋值为0,n赋值2,给循环变量i赋值1.
此时判断框中的条件不满足,执行S=0+$\frac{1}{2}$,n=2+2=4,i=1+1=2;
此时判断框中的条件不满足,执行S=0+$\frac{1}{2}$+$\frac{1}{4}$,n=4+2=6,i=2+1=3;
此时判断框中的条件不满足,执行S=0+$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$,n=6+2=8,i=3+1=4;
…
此时判断框中的条件不满足,执行S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2018}$,n=2020,i=1010;
此时判断框中的条件满足,
故判断框内应填入的一个条件为i>1009.
故选:A.
点评 本题考查了循环结构,是直到型循环,区别当型和直到型的关键在于是满足条件执行循环还是不满足条件执行循环,满足条件执行循环的是当型结构,不满足条件执行循环的是直到型结构,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x≥2}\\{x+y≥4}\\{2x-y-12≤0}\end{array}\right.$,则目标函数z=3x+y的最小值为( )
| A. | -8 | B. | -2 | C. | 8 | D. | $\frac{44}{3}$ |
14.“Z=$\frac{1}{sinθ+cosθ•i}$-$\frac{1}{2}$(其中i是虚数单位)是纯虚数.”是“θ=$\frac{π}{6}$+2kπ”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
11.已知非零向量$\overrightarrow m$,$\overrightarrow n$满足|$\overrightarrow m|=2|\overrightarrow n|$,cos<$\overrightarrow m,\overrightarrow n>=\frac{1}{3}$,若$\overrightarrow m⊥(t\overrightarrow n+\overrightarrow m)$,则实数t的值为( )
| A. | -6 | B. | $-\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
18.若等比数列{an}的公比为q,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{a_1}x+{a_3}y=2\\{a_2}x+{a_4}y=1\end{array}\right.$的解的情况下列说法正确的是( )
| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当$q=\frac{1}{2}$时,方程组有无穷多解 | |
| D. | 当且仅当$q=\frac{1}{2}$时,方程组无解 |
8.已知直线a⊥平面α,则“直线b∥平面α”是“直线a⊥直线b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
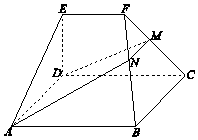 如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.
如图,在几何体ABCDEF中,底面ABCD为矩形,EF∥CD,AD⊥FC.点M在棱FC上,平面ADM与棱FB交于点N.