题目内容
四棱锥P-ABCD中底面ABCD是菱形,PA=PC,AC与BD交于点O.
(1)求证:PB⊥AC;
(2)若平面PAC⊥平面ABCD,∠ABC=60°,PB=AB=2,求点O到平面PBC的距离.
(1)求证:PB⊥AC;
(2)若平面PAC⊥平面ABCD,∠ABC=60°,PB=AB=2,求点O到平面PBC的距离.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)首先利用四棱锥P-ABCD中底面ABCD是菱形,PA=PC,AC与BD交于点O,得到:OP⊥AC,AC⊥BD
进一步得到:AC⊥平面PBD,PB?平面PBD,所以:PB⊥AC
(2)利用(1)的部分结论:平面PAC⊥平面ABCD,OP⊥平面ABCD,进一步求得:OP=
AC=2
AO=CO=
,利用VP-OBC=VO-PBC,求得:O到平面PBC的距离.
进一步得到:AC⊥平面PBD,PB?平面PBD,所以:PB⊥AC
(2)利用(1)的部分结论:平面PAC⊥平面ABCD,OP⊥平面ABCD,进一步求得:OP=
| 3 |
| 3 |
| 3 |
解答:
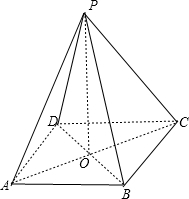
(1)证明:连结OP,
因为四棱锥P-ABCD中底面ABCD是菱形,PA=PC,AC与BD交于点O
所以:OP⊥AC,AC⊥BD
AC⊥平面PBD
PB?平面PBD
所以:PB⊥AC
(2)解:平面PAC⊥平面ABCD,
OP⊥平面ABCD
∵∠ABC=60°,PB=AB=2
∴OP=
AC=2
AO=CO=
∴进一步得到△PBC为等边三角形
所以:VP-OBC=VO-PBC
设点O到平面PBC的距离为h
∴
•
•1•
•
=
•
•2•2•
h
h=

(1)证明:连结OP,
因为四棱锥P-ABCD中底面ABCD是菱形,PA=PC,AC与BD交于点O
所以:OP⊥AC,AC⊥BD
AC⊥平面PBD
PB?平面PBD
所以:PB⊥AC
(2)解:平面PAC⊥平面ABCD,
OP⊥平面ABCD
∵∠ABC=60°,PB=AB=2
∴OP=
| 3 |
| 3 |
| 3 |
∴进一步得到△PBC为等边三角形
所以:VP-OBC=VO-PBC
设点O到平面PBC的距离为h
∴
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
h=
| ||
| 2 |
点评:本题考查的知识要点:线线垂直与线面垂直的转化,线面垂直的判定和性质,面面垂直的性质,利用几何体的体积相等等相关的运算问题.

练习册系列答案
相关题目
已知tanα=-2,α∈(-
,0),则cosα的值为( )
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
函数y=
的定义域为( )
| ||
| x |
A、(-∞,
| ||
B、(-∞,
| ||
C、(0,
| ||
D、(-∞,0)∪(0,
|
设全集U=R,集合M={y|y=x2+2,x∈U},集合N={y|y=10-3x,x∈M},则M∪N等于( )
| A、{1,3,2,6} |
| B、{x|2≤x≤4} |
| C、R |
| D、∅ |