题目内容
【题目】已知等差数列{an}的前n项和为Sn ， 若Sm﹣1=﹣4，Sm=0，Sm+2=14（m≥2，且m∈N*）
（Ⅰ）求m的值；
（Ⅱ）若数列{bn}满足 
=log2bn（n∈N+），求数列{（an+6）bn}的前n项和．
【答案】解：（Ⅰ）∵Sm﹣1=﹣4，Sm=0，Sm+2=14， ∴am=Sm﹣Sm﹣1=4，am+1+am+2=Sm+2﹣Sm=14，
设数列{an}的公差为d，则2am+3d=14，
∴d=2．
∵Sm= 
×m=0，∴a1=﹣am=﹣4，
∴am=﹣4+2（m﹣1）=4，
解得m=5．
（Ⅱ）由（Ⅰ）知an=﹣4+2（n﹣1）=2n﹣6，
∴n﹣3=log2bn ， 即bn=2n﹣3 ．
∴（an+6）bn=2n2n﹣3=n2n﹣2 ．
设数列{（an+6）bn}的前n项和为Tn ，
∴Tn=1× 
+2×1+3×2+…+…n2n﹣2 ， ①
∴2Tn=1×1+2×2+3×22+…+n2n﹣1 ， ②
① ﹣②，得﹣Tn= +1+2+…+2n﹣2﹣n2n﹣1
= 
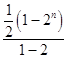﹣n2n﹣1
=（1﹣n）2n﹣1﹣ ．
∴Tn=（n﹣1）2n﹣1+
【解析】（I）计算am ， am+1+am+2 ， 利用等差数列的性质计算公差d，再代入求和公式计算m；（II）求出an ， bn ， 得出数列{（an+6）bn}的通项公式，利用错位相减法计算．
【考点精析】关于本题考查的数列的前n项和和数列的通项公式，需要了解数列{an}的前n项和sn与通项an的关系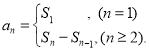
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能得出正确答案．
练习册系列答案
相关题目
