题目内容
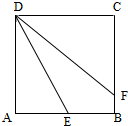
正方形ABCD的边长为2,点E、F分别在边AB、BC上,且AE=1,BF=
,将此正方形沿DE、DF折起,使点A、C重合于点P,则三棱锥P-DEF的体积是 .
| 1 |
| 2 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:根据题意得DP⊥面PEF,由此利用VP-DEF=VD-PEF,能求出三棱锥P-DEF的体积.
解答:
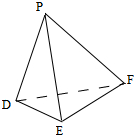
 解:根据题意知DP⊥PE,DP⊥PF,PE∩PF=P,
解:根据题意知DP⊥PE,DP⊥PF,PE∩PF=P,
∴DP⊥面PEF,
而DP=2,EF=
=
,PE=1,
PF=2-
=
,
由余弦定理得cos∠PEF=
=0,
∴sin∠PEF=1,
∴S△EPF=
PE•EF=
×1×
=
,
∴VP-DEF=VD-PEF=
×2×
=
.
故答案为:
.
 解:根据题意知DP⊥PE,DP⊥PF,PE∩PF=P,
解:根据题意知DP⊥PE,DP⊥PF,PE∩PF=P,∴DP⊥面PEF,
而DP=2,EF=
| BE2+BF2 |
| ||
| 2 |
PF=2-
| 1 |
| 2 |
| 3 |
| 2 |
由余弦定理得cos∠PEF=
1+
| ||||
2×1×
|
∴sin∠PEF=1,
∴S△EPF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴VP-DEF=VD-PEF=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 6 |

故答案为:
| ||
| 6 |
点评:本题考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
函数f(x)=
的定义域是( )
| 1 | ||
|
| A、(0,+∞) |
| B、[0,+∞) |
| C、[3,+∞) |
| D、(3,+∞) |
已知函数y=f(x)的定义域为(-π,π),且函数y=f(x+
)的图象关于直线x=-
对称,当x∈(0,π)时,f(x)=-f′(
)sinx-πlnx,其中f′(x)是y=f(x)的导函数,若a=f(30.3),b=f(logπ3),c=f(log2
),则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| 4 |
| A、a<b<c |
| B、c<a<b |
| C、b<a<c |
| D、c<b<a |
已知函数f(x)=
+x(a∈R)在[2,+∞)上单调递增,则a的取值范围是( )
| a |
| x |
| A、(0,4) |
| B、(-∞,4] |
| C、(0,2) |
| D、(-∞,2] |
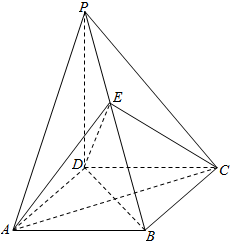 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=