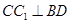题目内容
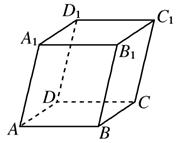
 如图,平行六面体ABCD-A1B1C1D1,若ABCD是边长为2的正方形,AA1=1,∠A1AD=∠A1AB=60°,则BD1的长为
如图,平行六面体ABCD-A1B1C1D1,若ABCD是边长为2的正方形,AA1=1,∠A1AD=∠A1AB=60°,则BD1的长为分析:由于平行六面体ABCD-A′B′C′D′的棱长都为1,底面ABCD为正方形,且AA′和AB与AD的夹角都等于60°,可以推出BB′⊥BD,求出BD 即可求解结果.
解答:解:平行六面体ABCD-A′B′C′D′的棱长都为1,底面ABCD为正方形,
且AA′和AB与AD的夹角都等于60°,那么AA′在底面ABCD上的射影垂直BD,
即BB′D′D是矩形,DB=
,所以对角线BD′=3
故答案为:3
且AA′和AB与AD的夹角都等于60°,那么AA′在底面ABCD上的射影垂直BD,
即BB′D′D是矩形,DB=
| 2 |
故答案为:3
点评:本题考查棱柱的结构特征,考查三垂线定理,解答关键是利用线面位置关系得到BB′D′D是矩形,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
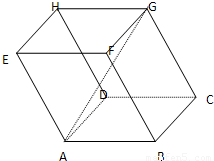
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.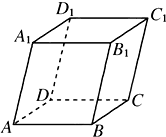 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,