题目内容
8.如图(1)所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,如图(2)所示,求这个正六棱柱容器容积最大值.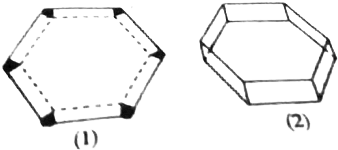
分析 要求正六棱柱容器的容积最大,得需要得出容积表达式;由柱体的体积公式知,底面积是正六边形,是六个全等小正△的和,高是Rt△中60°角所对的直角边,由高和底面积得出容积函数,用求导法可以求出最大值时的自变量取值.
解答 解:如图示: ,
,
设底面六边形的边长为x,高为d,则
d=$\sqrt{3}$•$\frac{1}{2}$(1-x); 又底面六边形的面积为:
S=6•$\frac{1}{2}$•x2•sin60°=$\frac{3\sqrt{3}}{2}$x2;所以,这个正六棱柱容器的容积为:
V=Sd=$\frac{3\sqrt{3}}{2}$x2•$\frac{\sqrt{3}}{2}$(1-x)=$\frac{9}{4}$(x2-x3),则对V求导,则
V′=$\frac{9}{4}$(2x-3x2),令V′=0,得x=0或x=$\frac{2}{3}$,
当0<x<$\frac{2}{3}$时,V′>0,V是增函数;当x>$\frac{2}{3}$时,V′<0,V是减函数;
∴x=$\frac{2}{3}$时,V有最大值,最大值是:$\frac{1}{3}$.
点评 本题通过建立体积函数表达式,由求导的方法求函数最大值,是比较常用的解题思路,也是中学数学的重要内容.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
19.函数g(x)的图象如图所示,下列数值排序正确的是( )
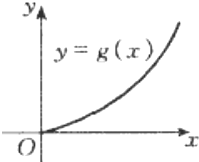

| A. | 0<g′(2)<g′(3)<g(3)-g(2) | B. | 0<g′(3)<g(3)-g(2)<g′(2) | C. | 0<g′(2)<g(3)-g(2)<g′(3) | D. | 0<g(3)-g(2)<g′(2)<g′(3) |
18.设集合A={x|-1≤x≤2},B={x|x<1且x∈Z},则A∩B=( )
| A. | {-1} | B. | {0} | C. | {-1,0} | D. | {0,1} |
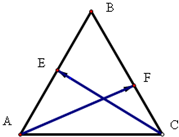 在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.
在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.