题目内容

2．已知等差数列{an}的前n项和为Sn，a8=1，S16=0，当Sn取最大值时n的值为（　　）
A．7B．8C．9D．10

分析 设公差为d，由a8=1，S16=0可求出d=-2，a1=15，即可得到an=17-2n，可得数列{an}前8项都是正数，以后各项都是负数，可得答案

解答 解：设公差为d，a8=1，S16=0，
∴S16=16a1+$\frac{16（16-1）d}{2}$=16a1+120d=0，a8=a1+7d=1，
∴d=-2，a1=15，
∴an=a1+（n-1）d=17-2n，
当an=17-2n≥0时，
即n≥8.5，
故当Sn取最大值时n的值为8，
故选：B．

点评 本题考查等差数列的前n项和公式，从数列的项的正负入手是解决问题的关键，属基础题．

练习册系列答案
相关题目
12．若a＞b＞0，证明：a2+$\frac{1}{（a-b）b}$≥4．
13．下列命题中，正确的序号是（2）．
（1）存在x0＞0，使得x0＜sinx0．
（2）若sinα≠$\frac{1}{2}$，则α≠$\frac{π}{6}$．
（3）“lna＞lnb”是“10a＞10b”的充要条件．
（4）若函数f（x）=x3+3ax2+bx+a2在x=-1有极值0，则a=2，b=9或a=1，b=3．
10．如图所示，在△ABC中，D为BC的中点，BP⊥DA，垂足为P，且$|{\overrightarrow{BP}}|=4$，则$\overrightarrow{BC}•\overrightarrow{BP}$=（　　）
A．4B．8C．16D．32
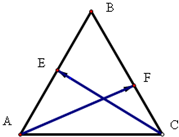17．在边长为1的正三角形ABC中，已知$\overrightarrow{AC}=\overrightarrow a，\overrightarrow{AB}$=$\overrightarrow b$，点E线段AB的中点，点F线段BC上，$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$．
（1）以$\overrightarrow a，\overrightarrow b$为基底表示$\overrightarrow{AF}，\overrightarrow{CE}$；
（2）求$\overrightarrow{AF}•\overrightarrow{CE}$．
7．在数列$\frac{{\sqrt{5}}}{3}，\frac{{\sqrt{10}}}{8}，\frac{{\sqrt{17}}}{a+b}，\frac{{\sqrt{a-b}}}{24}，\frac{{\sqrt{37}}}{35}，…$中，则实数a=$\frac{41}{2}$，b=$\frac{11}{2}$．
14．直线y=-$\sqrt{3}$x+3的倾斜角的大小为120°．
11．已知向量$\overrightarrow{a}$=（3，4），则与$\overrightarrow{a}$方向相同的单位向量是（　　）
A．（$\frac{4}{5}$，$\frac{3}{5}$）B．（$\frac{3}{5}$，$\frac{4}{5}$）C．（-$\frac{3}{5}$-，$\frac{4}{5}$）D．（4，3）
12．数列1，4，7，10，…，的第8项等于22．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网