题目内容
设f(n)=
+
+
+…+
(n∈N+)则f(k+1)-f(k)=( )
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:函数的值
专题:计算题
分析:根据题意求出f(k+1)和f(k),再求出 f(k+1)-f(k)并化简即可.
解答:
解:由题意得,f(k+1)=
+
+
+…+
,
f(k)=
+
+
+…+
,
所以f(k+1)-f(k)=
+
-
=
-
,
故选:B.
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| k+4 |
| 1 |
| 2(k+1) |
f(k)=
| 1 |
| k+1 |
| 1 |
| k+2 |
| 1 |
| k+3 |
| 1 |
| 2k |
所以f(k+1)-f(k)=
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
故选:B.
点评:本题考查函数的值,关键是清楚解析式的特点以及变化规律,属于基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知点A(2,
)关于极点对称的点的极坐标为( )
| 5π |
| 4 |
A、(2,
| ||
B、(2,
| ||
C、(-2,
| ||
D、(-2,
|
若tan(2π+α)=-
,则
的值是( )
| 1 |
| 2 |
| 2sinαcosα |
| sin2α-cos2α |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
圆心为(1,-1),半径为5的圆的标准方程为( )
| A、(x-1)2+(y+1)2=5 |
| B、(x+1)2+(y-1)2=5 |
| C、(x-1)2+(y+1)2=25 |
| D、(x+1)2+(y-1)2=25 |
下列各组函数表示相等函数的是( )
A、y=
| |||
B、y=
| |||
| C、y=x0与 y=1 | |||
D、y=
|
随机变量X的概率分布规律为P(X=n)=
(n=1,2,3),其中a是常数,则P(1≤X≤2)的值为( )
| a |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
类比三角形中的性质:
(1)两边之和大于第三边;
(2)中位线长等于底边的一半;
(3)三内角平分线交于一点;
可得四面体的对应性质:
(1)任意三个面的面积之和大于第四个面的面积;
(2)过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的
;
(3)四面体的六个二面角的平分面交于一点.
其中类比推理结论正确的有( )
(1)两边之和大于第三边;
(2)中位线长等于底边的一半;
(3)三内角平分线交于一点;
可得四面体的对应性质:
(1)任意三个面的面积之和大于第四个面的面积;
(2)过四面体的交于同一顶点的三条棱的中点的平面面积等于第四个面面积的
| 1 |
| 4 |
(3)四面体的六个二面角的平分面交于一点.
其中类比推理结论正确的有( )
| A、(1) |
| B、(1)(2) |
| C、(1)(2)(3) |
| D、都不对 |
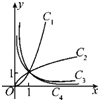 图中的曲线是幂函数y=xn在第一象限的图象,已知n可取±2,±
图中的曲线是幂函数y=xn在第一象限的图象,已知n可取±2,±| 1 |
| 2 |
A、-2,-
| ||||
B、2,
| ||||
C、-
| ||||
D、2,
|