题目内容
20.如图,在正方体AC1中,A1E1=CE,A1F1=CF.求证:E1F1$\underset{∥}{=}$EF.
分析 在AD上取点G,使AG=A1E1=CE,在AB上取点H,使AH=A1F1=CF,从而△HAG≌△FCE≌△F1A1E1,由此能证明E1F1$\underset{∥}{=}$EF.
解答 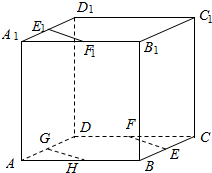 证明:在AD上取点G,使AG=A1E1=CE,
证明:在AD上取点G,使AG=A1E1=CE,
在AB上取点H,使AH=A1F1=CF,
∵∠HAG=∠FCE=∠F1A1E1,
∴△HAG≌△FCE≌△F1A1E1,
∴HG=FE=F1E1,
∵A1E1$\underset{∥}{=}$AG,A1F1$\underset{∥}{=}$AH,∴F1E1∥HG,
∵AG$\underset{∥}{=}$CE,AH$\underset{∥}{=}$CF,∴HG∥EF,
∴E1F1$\underset{∥}{=}$EF.
点评 本题考查两直线平行且相等的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
10.三个数0.67,70.6,log0.67的大小关系为( )
| A. | ${0.6^7}<{log_{0.6}}7<{7^{0.6}}$ | B. | 0.67<70.6<log0.67 | ||
| C. | ${log_{0.6}}7<{7^{0.6}}<{0.6^7}$ | D. | ${log_{0.6}}7<{0.6^7}<{7^{0.6}}$ |
10.已知sin(π-θ)cosθ<0,且|cosθ|=cosθ,则角θ是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |