题目内容
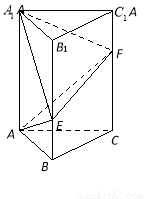
(本小题满分10分)如图,在直三棱柱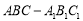 中,已知
中,已知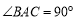 ,
,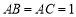 ,
,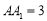 ,点
,点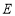 ,
,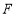 分别在棱
分别在棱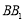 ,
,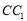 上,且
上,且 ,
,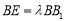 ,
,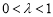 .
.
(1)当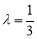 时,求异面直线
时,求异面直线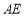 与
与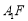 所成角的大小;
所成角的大小;
(2)当直线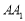 与平面
与平面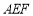 所成角的正弦值为
所成角的正弦值为 时,求
时,求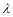 的值.
的值.
(1) (2)
(2) .
.
【解析】
试题分析:(1)利用空间向量求异面直线所成角,关键明确各点坐标,利用空间向量数量积求夹角: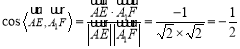 ,又异面直线
,又异面直线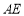 与
与 所成角不为钝角,所以异面直线
所成角不为钝角,所以异面直线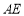 与
与 所成角为
所成角为 .(2)利用空间向量表示线面角,关键求出平面的法向量,再利用直线与平面所成角的正弦值等于直线与平面法向量所成角余弦值的绝对值求解. 平面
.(2)利用空间向量表示线面角,关键求出平面的法向量,再利用直线与平面所成角的正弦值等于直线与平面法向量所成角余弦值的绝对值求解. 平面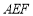 的法向量
的法向量 满足
满足 ,且
,且 .所以
.所以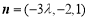 ,
,
 ,解得
,解得
试题解析:建立如图所示的空间直角坐标系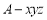 .
.
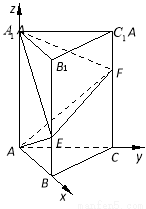
(1)因为AB=AC=1, 3,
3, ,
,
所以各点的坐标为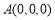 ,
, ,
, ,
,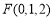 .
.
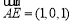 ,
, . 2分
. 2分
因为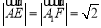 ,
,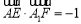 ,
,
所以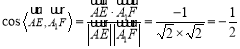 .所以向量
.所以向量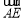 和
和 所成的角为
所成的角为 ,
,
所以异面直线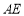 与
与 所成角为
所成角为 . 4分
. 4分
(2)因为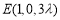 ,
,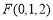 ,所以
,所以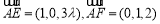 .
.
设平面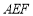 的法向量为
的法向量为 ,
,
则 ,且
,且 .
.
即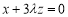 ,且
,且 .令
.令 ,则
,则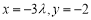 .
.
所以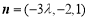 是平面
是平面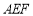 的一个法向量. 6分
的一个法向量. 6分
又 ,则
,则 ,
,
又因为直线 与平面
与平面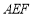 所成角的正弦值为
所成角的正弦值为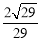 ,
,
所以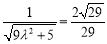 ,解得,
,解得, . 10分
. 10分
考点:利用空间向量求线线角、线面角

练习册系列答案
相关题目
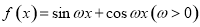 的最小正周期为
的最小正周期为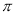 ,将
,将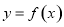 的图象向左平移
的图象向左平移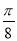 个单位得函数
个单位得函数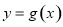 的图象,则
的图象,则 上单调递减
上单调递减 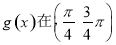 上单调递减
上单调递减 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则关于
,则关于 的不等式
的不等式 的解集是 .
的解集是 . 的值是 .
的值是 .
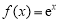 (其中
(其中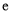 是自然对数的底数),
是自然对数的底数),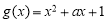 ,
,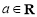 .
.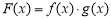 ,且
,且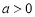 ,求
,求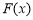 的单调增区间;
的单调增区间;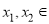
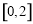 ,
,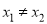 ,均有
,均有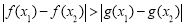 成立,求实数
成立,求实数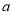 的取值范围.
的取值范围. 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则关于
,则关于 的不等式
的不等式 的解集是 .
的解集是 . 的底面ABCD是平行四边形,
的底面ABCD是平行四边形, 底面ABCD,
底面ABCD,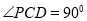 ,
,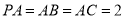 .
.
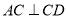 ;
; 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.