题目内容
(本小题满分12分)如图,四棱锥 的底面ABCD是平行四边形,
的底面ABCD是平行四边形, 底面ABCD,
底面ABCD,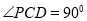 ,
,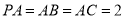 .
.

(1)求证: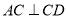 ;
;
(2)点E是棱PC的中点,求点B到平面EAD的距离.
(1)证明详见解析;(2) .
.
【解析】
试题分析:本题主要考查线线垂直、线面垂直、点到面的距离等基础知识,同时考查分析问题解决问题的能力、推理论证能力、运算求解能力. 第一问,利用线面垂直“PA⊥底面ABCD”的性质可得PA⊥CD,而PC⊥CD,则利用线面垂直的判定可得CD⊥平面PAC,所以CD垂直于面PAC内的线;第二问,由于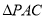 为等腰三角形,所以AE⊥PC,且
为等腰三角形,所以AE⊥PC,且 ,利用第一问中的结论,可知AE⊥CD,利用线面垂直的判定得AE⊥平面PCD,作辅助线CF⊥DE,则可得CF⊥平面EAD,从而可判定CF即为点C到面EAD的距离,在
,利用第一问中的结论,可知AE⊥CD,利用线面垂直的判定得AE⊥平面PCD,作辅助线CF⊥DE,则可得CF⊥平面EAD,从而可判定CF即为点C到面EAD的距离,在 中解出CF的长即可.
中解出CF的长即可.
试题解析:(Ⅰ)证明:
因为PA⊥底面ABCD,所以PA⊥CD,
因为∠PCD=90,所以PC⊥CD,
所以CD⊥平面PAC,
所以CD⊥AC. …4分
(Ⅱ)因为PA=AB=AC=2,E为PC的中点,所以AE⊥PC, .
.
由(Ⅰ)知AE⊥CD,所以AE⊥平面PCD.
作CF⊥DE,交DE于点F,则CF⊥AE,则CF⊥平面EAD.
因为BC∥AD,所以点B与点C到平面EAD的距离相等,
CF即为点C到平面EAD的距离. …8分
在Rt△ECD中,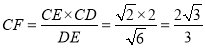 .
.
所以,点B到平面EAD的距离为 . …12分
. …12分

考点:线线垂直、线面垂直、点到面的距离.

练习册系列答案
相关题目
 的公比
的公比 ,
, ,
, ,则
,则 前5项和
前5项和 等于
等于 (B)
(B)
 (D)
(D)
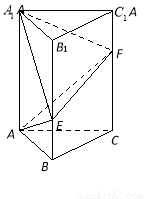
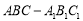 中,已知
中,已知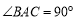 ,
,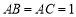 ,
,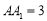 ,点
,点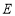 ,
,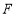 分别在棱
分别在棱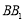 ,
,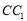 上,且
上,且 ,
,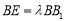 ,
,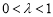 .
. 
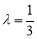 时,求异面直线
时,求异面直线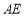 与
与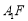 所成角的大小;
所成角的大小;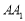 与平面
与平面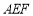 所成角的正弦值为
所成角的正弦值为 时,求
时,求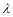 的值.
的值.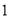 ,
,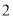 ,
,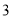 的三个盒子中,每个盒子的放球数量不限,则在
的三个盒子中,每个盒子的放球数量不限,则在 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为 ,斜率为
,斜率为 的直线
的直线 交y轴于点
交y轴于点 .
.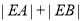 .
. (i为虚数单位),则
(i为虚数单位),则 .
. ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 (i为虚数单位),则
(i为虚数单位),则 .
. 弦被点A(1,1)平分,那么这条弦所在的直线方程是 ;
弦被点A(1,1)平分,那么这条弦所在的直线方程是 ;