题目内容
已知函数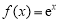 (其中
(其中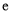 是自然对数的底数),
是自然对数的底数),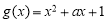 ,
,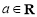 .
.
(1)记函数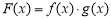 ,且
,且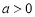 ,求
,求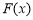 的单调增区间;
的单调增区间;
(2)若对任意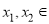
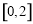 ,
,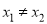 ,均有
,均有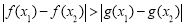 成立,求实数
成立,求实数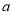 的取值范围.
的取值范围.
(1) 和
和 ;(2)
;(2)
【解析】
试题分析:(1)利用导数求函数单调性:先求函数导数 ,再解不等式
,再解不等式 得
得 或
或 ,从而
,从而 的单调增区间为
的单调增区间为 和
和 ,(2)解决不等式恒成立问题,关键在于转化:先根据单调性去绝对值,设
,(2)解决不等式恒成立问题,关键在于转化:先根据单调性去绝对值,设 ,根据
,根据 在
在 上单调递增,所以有
上单调递增,所以有 对
对 恒成立,再根据绝对值不等式化简为
恒成立,再根据绝对值不等式化简为
 对
对
 ,
, 恒成立,整理为
恒成立,整理为
 对
对
 ,
, 恒成立,即
恒成立,即 和
和 在
在 都是单调递增函数,最后根据函数最值求
都是单调递增函数,最后根据函数最值求 的取值范围
的取值范围
试题解析:(1)因为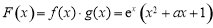 ,
,
所以 , 2分
, 2分
令 ,因为
,因为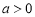 ,得
,得 或
或 , 5分
, 5分
所以 的单调增区间为
的单调增区间为 和
和 ; 6分
; 6分
(2)因为对任意
 且
且 ,均有
,均有 成立,
成立,
不妨设 ,根据
,根据 在
在 上单调递增,
上单调递增,
所以有 对
对 恒成立, 8分
恒成立, 8分
所以 对
对
 ,
, 恒成立,
恒成立,
即 对
对
 ,
, 恒成立,
恒成立,
所以 和
和 在
在 都是单调递增函数, 11分
都是单调递增函数, 11分
当 在
在 上恒成立,
上恒成立,
得 在
在 恒成立,得
恒成立,得 在
在 恒成立,
恒成立,
因为 在
在 上单调减函数,所以
上单调减函数,所以 在
在 上取得最大值
上取得最大值 ,
,
解得 . 13分
. 13分
当 在
在 上恒成立,
上恒成立,
得 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立,
上恒成立,
因为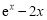 在
在 上递减,在
上递减,在 上单调递增,
上单调递增,
所以 在
在 上取得最小值
上取得最小值 ,
,
所以 , 15分
, 15分
所以实数 的取值范围为
的取值范围为 . 16分
. 16分
考点:利用导数求函数单调区间,不等式恒成立问题

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
 的虚部为__________.
的虚部为__________.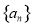 的公比为2,若
的公比为2,若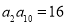 ,则
,则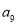 的值是
的值是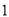 ,
,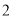 ,
, 的三个盒子中,每个盒子的放球数量不限,则在
的三个盒子中,每个盒子的放球数量不限,则在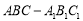 中,已知
中,已知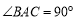 ,
,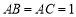 ,
,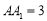 ,点
,点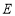 ,
,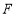 分别在棱
分别在棱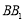 ,
,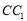 上,且
上,且 ,
,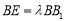 ,
,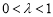 .
. 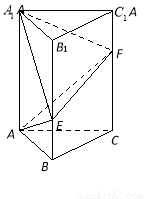
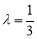 时,求异面直线
时,求异面直线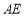 与
与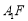 所成角的大小;
所成角的大小;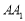 与平面
与平面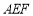 所成角的正弦值为
所成角的正弦值为 时,求
时,求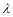 的值.
的值.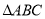 中,
中,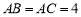 ,
,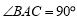 ,
, 是
是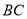 的中点,若向量
的中点,若向量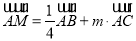 ,且
,且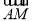 的终点
的终点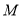 在
在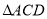 的内部(不含边界),则
的内部(不含边界),则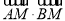 的取值范围是 .
的取值范围是 .
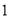 ,
,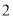 ,
,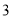 的三个盒子中,每个盒子的放球数量不限,则在
的三个盒子中,每个盒子的放球数量不限,则在 (i为虚数单位),则
(i为虚数单位),则 .
. 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 .
. 的值;
的值; 的值.
的值.