题目内容
O为△ABC的外心，AB=4，AC=2，则
•
的值为 ．
| AO |
| BC |
分析：如图所示，取线段BC的中点，连接OD，AD．利用三角形的外心的性质和向量形式的中点坐标公式可得OD⊥BC，
=
(
+
)．再利用向量的三角形法则即可得到
•
=
(
+
)•(
-
)，化简代入即可．
| AD |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB |
解答：解：如图所示，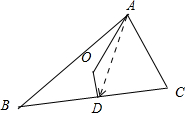
取线段BC的中点，连接OD，AD．
则OD⊥BC，
=
(
+
)．
∵
=
+
，
=
-
．
∴
•
=(
+
)•
=
•
+
•
=
•
=
(
+
)•(
-
)
=
(
2-
2)
=
(22-42)=-6．
故答案为-6．
取线段BC的中点，连接OD，AD．则OD⊥BC，
| AD |
| 1 |
| 2 |
| AB |
| AC |
∵
| AO |
| AD |
| DO |
| BC |
| AC |
| AB |
∴
| AO |
| BC |
| AD |
| DO |
| BC |
=
| AD |
| BC |
| DO |
| BC |
=
| AD |
| BC |
=
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB |
=
| 1 |
| 2 |
| AC |
| AB |
=
| 1 |
| 2 |
故答案为-6．
点评：熟练掌握三角形的外心的性质和向量形式的中点坐标公式、向量的三角形法则及平行四边形法则是解题的关键．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
如图，已知O为△ABC的外心，a，b，c分别是角A、B、C的对边，且满足
（2009•湖北模拟）如图在△ABC中，AB=3，BC=