题目内容
（2013•崇明县二模）已知O为△ABC的外心，AB=4，AC=2，∠BAC为钝角，M是边BC的中点，则
•
的值等于
| AM |
| AO |
5
5
．分析：过点O分别作OE⊥AB于E，OF⊥AC于F，可得E、F分别是AB、AC的中点．根据Rt△AOE中余弦的定义，算出
•
=
2=8，同理得
•
=
2=2．再由M是BC边的中点，可得
•
=
(
+
)•
=
（8+2）=5．
| AB |
| AO |
| 1 |
| 2 |
| |AB| |
| AC |
| AO |
| 1 |
| 2 |
| |AC| |
| AM |
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| 1 |
| 2 |
解答：解：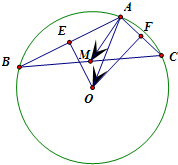
过点O分别作OE⊥AB于E，OF⊥AC于F，则E、F分别是AB、AC的中点
可得Rt△AEO中，cos∠OAE=
=
∴
•
=
•
•
=
2=8，
同理可得
•
=
2=2
∵M是BC边的中点，可得
=
(
+
)，
∴
•
=
(
+
)•
=
（
•
+
•
）=
×10=5
故答案为：5
过点O分别作OE⊥AB于E，OF⊥AC于F，则E、F分别是AB、AC的中点可得Rt△AEO中，cos∠OAE=
| ||
|
| ||
2
|
∴
| AB |
| AO |
| |AB| |
| |AO| |
| ||
2
|
| 1 |
| 2 |
| |AB| |
同理可得
| AC |
| AO |
| 1 |
| 2 |
| |AC| |
∵M是BC边的中点，可得
| AM |
| 1 |
| 2 |
| AB |
| AC |
∴
| AM |
| AO |
| 1 |
| 2 |
| AB |
| AC |
| AO |
| 1 |
| 2 |
| AB |
| AO |
| AC |
| AO |
| 1 |
| 2 |
故答案为：5
点评：本题将△ABC放在它的外接圆O中，求中线AM对应的向量
与
的数量积之值，着重考查了平面向量的数量积的运算性质和三角形外接圆等知识，属于中档题．
| AM |
| AO |
练习册系列答案
阅读快车系列答案
相关题目