题目内容
某同学参加高二学业水平测试的 4 门必修科目考试,已知该同学每门学科考试成绩达到“A”等级的概率均为 ,且每门考试成绩的结果互不影响.
,且每门考试成绩的结果互不影响.
(1) 求该同学至少得到两个“A”的概率;
(2) 已知在高考成绩计分时,每有一科达到“A”,则高考成绩加 1 分,如果 4 门学科均达到“A”,则高考成绩额外再加 1 分.现用随机变量 Y 表示该同学学业水平测试的总加分,求 Y 的概率分布列和数学期望.
解:(1)设4门考试成绩得到“A”的次数为X ,依题意,随机变量X~B(4,
,依题意,随机变量X~B(4, ),
),
则P(X³2)=1-P(X=0)-P(X=1)=1- =
= ,
,
故该同学至少得到两个“A”的概率为 . ……………6分
. ……………6分
(2)随机变量Y的可能值为0,1,2,3,5,则 ………7分
P(Y=0)= =
= , P(Y=1)=
, P(Y=1)= =
= ,
,
P(Y=2)= =
= , P(Y=3)=
, P(Y=3)= =
= ,
,
P(Y=5)= =
= .
.
随机变量Y的概率分布如下表所示
| Y | 0 | 1 | 2 | 3 | 5 |
| P |
|
|
|
|
|
从而E(Y)=0´ +1´
+1´ +2´
+2´ +3´
+3´ +5´
+5´ =
= . ………………1
. ………………1 4分
4分

练习册系列答案
相关题目
 边
边 形OABC,OB=OC,
形OABC,OB=OC, 且∠AOB=∠AOC=
且∠AOB=∠AOC= ,则cos〈
,则cos〈 ,
, 〉的值为
〉的值为 
 医疗队,如果要求内科医生和外科医生中都有人参加,则有 种选法(用数字作答).
医疗队,如果要求内科医生和外科医生中都有人参加,则有 种选法(用数字作答). 的概率分布如下:
的概率分布如下:
 .
. a+bi)2= .
a+bi)2= . ,
, ,
, ,
, ,
, ……………………………
…………………………… ,
,
 ,则
,则 .
. 是由正数组成的等比数列,
是由正数组成的等比数列,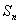 表示数列
表示数列 项的和,
项的和, 若
若 ,
, ,则
,则 的值为( )
的值为( ) B.69 C.93 D.189
B.69 C.93 D.189