Question

在△ABC中，A，B都是锐角，且sin²A+sin²B=1，AC=3，则

AC

•

BA

=

 

．

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：在△ABC中，A，B都是锐角，且sin²A+sin²B=1，利用同角三角函数的平方关系可得sinA=cosB=sin(

π

2

-B)，由于A，

π

2

-B都为锐角，可得A+B=

π

2

．于是

AC

•

CB

=0．再利用向量的三角形法则和数量积运算即可得出：

AC

•

BA

=

AC

•(

CA

-

CB

)=-

AC

2．

解答： 解：∵在△ABC中，A，B都是锐角，且sin²A+sin²B=1，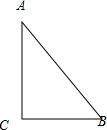
∴sin²A=1-sin²B=cos²B，∴sinA=cosB=sin(

π

2

-B)，
∵A，

π

2

-B都为锐角，∴A=

π

2

-B，即A+B=

π

2

．
∴

AC

•

CB

=0．
∴

AC

•

BA

=

AC

•(

CA

-

CB

)=-

AC

2=-9．
故答案为：-9．

点评：本题考查了同角三角函数的平方关系、向量的三角形法则和数量积运算，考查了推理能力和计算能力，属于中档题．