题目内容
观察下列两个结论:
(Ⅰ)若a,b∈R+,且a+b=1,则
+
≥4;
(Ⅱ)若a,b,c∈R+,且a+b+c=1,则
+
+
≥9;先证明结论(Ⅱ),再类比(Ⅰ)(Ⅱ)结论,请你写出一个关于n个正数a1,a2,a3,…,an的结论?(写出结论,不必证明.)
(Ⅰ)若a,b∈R+,且a+b=1,则
| 1 |
| a |
| 1 |
| b |
(Ⅱ)若a,b,c∈R+,且a+b+c=1,则
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
由柯西不等式(1+1+1)2≤(a+b+c)(
+
+
),
得32≤1×(
+
+
),
所以
+
+
≥9,
类比(Ⅰ)(Ⅱ)结论,写出一个关于n个正数a1,a2,a3,…,an的结论是:
若ai∈R+(i=1,2,3,…,n),且
ai=1,则
≥n2.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
得32≤1×(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
所以
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
类比(Ⅰ)(Ⅱ)结论,写出一个关于n个正数a1,a2,a3,…,an的结论是:
若ai∈R+(i=1,2,3,…,n),且
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| 1 |
| ai |

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 满足
满足 且
且
 .
.
 ;
;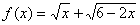 .
.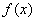 最大值?
最大值?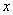 使
使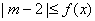 成立,求实数
成立,求实数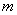 的取值范围。
的取值范围。 .
. (Ⅰ)当
(Ⅰ)当 时,求函数
时,求函数 的最小值;
的最小值;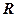 时,求实数
时,求实数 的取值范围。
的取值范围。 ,求
,求 的最大值
的最大值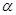 和
和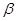 可以有不在同一条直线上的三个公共点
可以有不在同一条直线上的三个公共点 ,比较
,比较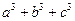 与
与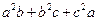 的大小。
的大小。 ;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( ) 



 ,圆心角为
,圆心角为 的扇形,则此圆锥的体积为 .
的扇形,则此圆锥的体积为 .