题目内容
已知函数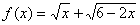 .
.
(1)求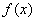 最大值?
最大值?
(2)若存在实数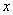 使
使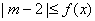 成立,求实数
成立,求实数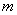 的取值范围。
的取值范围。
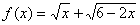 .
.(1)求
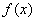 最大值?
最大值?(2)若存在实数
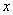 使
使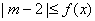 成立,求实数
成立,求实数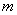 的取值范围。
的取值范围。(1)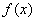 最大值是3.(2)实数
最大值是3.(2)实数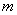 的取值范围
的取值范围 。
。
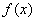 最大值是3.(2)实数
最大值是3.(2)实数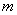 的取值范围
的取值范围 。
。试题分析:(1)由柯西不等式有
 当且仅当
当且仅当 ,即
,即 时,等号成立。所以,
时,等号成立。所以,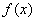 最大值的是3.
最大值的是3.(2)依题意,只须
 ,由(1)得,
,由(1)得, ,解得
,解得 。所以,实数
。所以,实数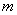 的取值范围
的取值范围 。
。点评:中档题,涉及不等式恒成立问题,往往应用“转化与化归思想”,将问题转化成求函数的最值问题,利用不等式或导数,求函数的最值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,且
,且 的解集为
的解集为 .
. 的值;
的值; ,且
,且 ,求
,求  的最小值.
的最小值. (an2+bn+c)
(an2+bn+c) 等于( ).
等于( ).



 ;
; .
. ≤a恒成立, 则a的最小值为
≤a恒成立, 则a的最小值为 

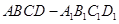 中,点
中,点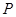 为线段
为线段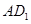 上一动点,点
上一动点,点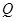 为底面
为底面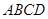 内(含边界)一动点,
内(含边界)一动点,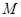 为
为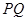 的中点,点
的中点,点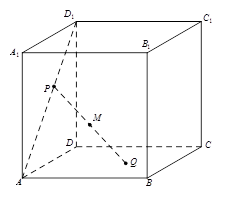
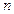 有关,若
有关,若 时该命题成立,那么可推得
时该命题成立,那么可推得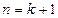 时该命题也成立,现在已知当
时该命题也成立,现在已知当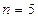 时该命题不成立,那么可推得
时该命题不成立,那么可推得 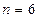 时,该命题不成立
时,该命题不成立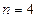 时,该命题不成立
时,该命题不成立