题目内容
11.给出下列结论:动点M(x,y)分别到两定点(-4,0),(4,0)连线的斜率之积为-$\frac{9}{16}$,设M(x,y)的轨迹为曲线C,F1、F2分别曲线C的左、右焦点,则下列命题中:(1)曲线C的焦点坐标为F1(-5,0)、F2(5,0);
(2)曲线C上存在一点M,使得S${\;}_{△{F}_{1}P{F}_{2}}$=9;
(3)P为曲线C上一点,P,F1,F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,$\frac{|P{F}_{1}|}{|P{F}_{2}|}$的值为$\frac{23}{9}$;
(4)设A(1,1),动点P在曲线C上,则|PA|-|PF2|的最大值为$\sqrt{9-2\sqrt{7}}$;
其中正确命题的序号是(3)(4).
分析 求出曲线C的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1,x≠±4.
在(1)中,C的焦点坐标为F1(-$\sqrt{7}$,0)、F2($\sqrt{7}$,0);在(2)中,(S${\;}_{△{F}_{1}P{F}_{2}}$)max=3$\sqrt{7}$<9;在(3)中,由椭圆定义得$\frac{|P{F}_{1}|}{|P{F}_{2}|}$的值为$\frac{23}{9}$;在(4)中,当P,F2,A共线时,|PA|-|PF2|的最大值为|AF2|.
解答 解:∵动点M(x,y)分别到两定点(-4,0),(4,0)连线的斜率之积为-$\frac{9}{16}$,
∴$\frac{y}{x+4}•\frac{y}{x-4}$=-$\frac{9}{16}$,整理,得曲线C的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1,x≠±4
在(1)中,∵F1、F2分别曲线C的左、右焦点,c=$\sqrt{16-9}$=$\sqrt{7}$,
∴线C的焦点坐标为F1(-$\sqrt{7}$,0)、F2($\sqrt{7}$,0),故(1)错误;
在(2)中,曲线C上存在一点M,(S${\;}_{△{F}_{1}P{F}_{2}}$)max=$\frac{1}{2}×2c×b$=bc=3$\sqrt{7}$<9,故(2)错误;
在(3)中,当∠PF2F1=90°时,|PF2|=$\frac{{b}^{2}}{a}$=$\frac{9}{4}$,|PF1|=8-$\frac{9}{4}$=$\frac{23}{4}$,$\frac{|P{F}_{1}|}{|P{F}_{2}|}$的值为$\frac{23}{9}$,故(3)正确;
在(4)中,当P,F2,A共线时,|PA|-|PF2|的最大值为|AF2|=$\sqrt{(1-0)^{2}+(1-\sqrt{7})^{2}}$=$\sqrt{9-2\sqrt{7}}$,故(4)正确.
故答案为:(3)(4).
点评 本题考查椭圆的定义标准方程及其性质、三角形的内切圆的性质、斜率计算公式,考查了转化能力,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{9}$ |
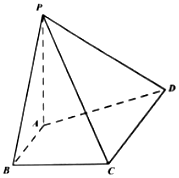 在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.
在四菱锥P-ABCD中,PA⊥AD,PA=1,PC=PD,底面ABCD是梯形,AB∥CD,AB⊥BC,AB=BC=1,CD=2.(I)求证:PA⊥AB;
(II)求直线AD与平面PCD所成角的大小.
| A. | 4 | B. | $-\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
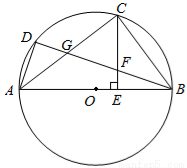
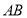 为圆
为圆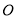 的直径,
的直径,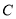 ,
,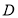 是圆
是圆 上的两个点,
上的两个点,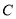 是劣弧
是劣弧 的中点,
的中点,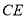 ⊥
⊥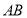 于
于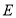 ,
,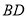 交
交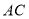 于
于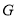 ,交
,交 于
于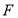 .
.
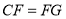 ;
; .
.