题目内容
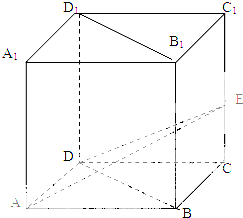 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点.(1)求证:BD⊥AE;
(2)求点A到平面BDE的距离.
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:(1)连AC,根据正方体的几何特征,可得CC1⊥BD,AC⊥BD,由线面垂直的判定定理,可得BD⊥平面ACE1,再根据线面垂直的性质,即可得到BD⊥AE.
(2)利用等体积法,求点A到平面BDE的距离.
(2)利用等体积法,求点A到平面BDE的距离.
解答:
(1)证明:连AC,则
∵正方体AC1中,CC1⊥平面ABCD,∴CC1⊥BD.
∵正方形ABCD,AC⊥BD且AC∩CC1=C.
∴BD⊥平面ACE,
∴AE?平面ACE,
∴BD⊥AE;
(2)解:设A到平面BDE的距离为h,则
∵棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,
∴BE=DE=
,BD=2
,
∴S△BDE=
,
∴
×
h=
×2×1,
∴h=
.
∵正方体AC1中,CC1⊥平面ABCD,∴CC1⊥BD.
∵正方形ABCD,AC⊥BD且AC∩CC1=C.
∴BD⊥平面ACE,
∴AE?平面ACE,
∴BD⊥AE;
(2)解:设A到平面BDE的距离为h,则
∵棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点,
∴BE=DE=
| 5 |
| 2 |
∴S△BDE=
| 6 |
∴
| 1 |
| 3 |
| 6 |
| 1 |
| 3 |
∴h=
| ||
| 3 |
点评:本题考查的知识点是线面垂直的性质,点到平面的距离,其中(1)的关键是熟练掌握空间线线、线面及面面之间位置关系的转化,(2)的关键是等体积转化.

练习册系列答案
相关题目
命题P:“若m>0,则方程x2+x-m=0有实数根”的否定是( )
| A、¬P:若m>0,则方程x2+x-m=0没有实数根 |
| B、¬P:若方程x2+x-m=0没有实数根,则m≤0 |
| C、¬P:若m≤0,则方程x2+x-m=0没有实数根 |
| D、¬P:若m<0,则方程x2+x-m=0没有实数根 |
若lg2=a,lg3=b,则log26=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
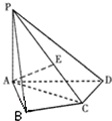 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.