题目内容
已知函数f(x)=(2+a)x+a2lnx,g(x)=x2+2x+b(a,b∈R).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同,若a>0,试建立b关于a的函数关系式,并求b的最小值;
(Ⅲ)设b=2a2+2a,若对任意给定的x0∈(0,1],总存在两个不同的xi(i=1,2),使得g(xi)+f(x0)=0成立,求a的取值范围.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同,若a>0,试建立b关于a的函数关系式,并求b的最小值;
(Ⅲ)设b=2a2+2a,若对任意给定的x0∈(0,1],总存在两个不同的xi(i=1,2),使得g(xi)+f(x0)=0成立,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出函数的定义域和导数,根据函数单调性和导数之间的关系即可求f(x)的单调区间;
(Ⅱ)求函数的导数,根据导数的几何意义,即可建立b关于a的函数关系式,并求b的最小值;
(Ⅲ)求函数的导数,根据存在两个不同的xi(i=1,2),使得g(xi)+f(x0)=0成立,建立条件关系即可得到结论.
(Ⅱ)求函数的导数,根据导数的几何意义,即可建立b关于a的函数关系式,并求b的最小值;
(Ⅲ)求函数的导数,根据存在两个不同的xi(i=1,2),使得g(xi)+f(x0)=0成立,建立条件关系即可得到结论.
解答:
解:(Ⅰ)∵f′(x)=2+a+
,x>0,
∴当2+a≥0,即a≥-2时,f′(x)>0,f(x)的单调递增区间是(0,+∞);
当2+a<0,即a<-2时,f(x)的单调递增区间是(0,-
),
单调递减区间是(-
,+∞).
(Ⅱ)设两曲线y=f(x)与y=g(x)的公共点为(x0,y0),
则
消去x0,得b=a2lna.
又b′=2a(lna+
),
故b=a2lna在(0,
)上递减,在(
,+∞)上递增.
故b的最小值为-
.
(III)当x0∈(0,1]时,f′(x)=2+a+
≥2+a+a2>0,
故f(x)在(0,1]上单调递增,
∴f(x0)∈(-∞,2+a],-f(x0)∈[-2-a,+∞).
由题意得,函数g(x)的最小值b-1=2a2+2a-1<-2-a,
∴2a2+3a+1>0,
∴-1<a<-
.
| a2 |
| x |
∴当2+a≥0,即a≥-2时,f′(x)>0,f(x)的单调递增区间是(0,+∞);
当2+a<0,即a<-2时,f(x)的单调递增区间是(0,-
| a2 |
| 2+a |
单调递减区间是(-
| a2 |
| 2+a |
(Ⅱ)设两曲线y=f(x)与y=g(x)的公共点为(x0,y0),
则
|
又b′=2a(lna+
| 1 |
| 2 |
故b=a2lna在(0,
| 1 | ||
|
| 1 | ||
|
故b的最小值为-
| 1 |
| 2e |
(III)当x0∈(0,1]时,f′(x)=2+a+
| a2 |
| x |
故f(x)在(0,1]上单调递增,
∴f(x0)∈(-∞,2+a],-f(x0)∈[-2-a,+∞).
由题意得,函数g(x)的最小值b-1=2a2+2a-1<-2-a,
∴2a2+3a+1>0,
∴-1<a<-
| 1 |
| 2 |
点评:本题主要考查函数单调性和导数之间的关系,以及导数的几何意义,要求熟练掌握导数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
棱长都是1的三棱锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中,定义域为(0,+∞)的函数是( )
| A、y=ex | ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
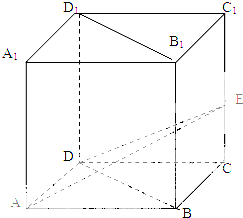 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点.