题目内容
在平面直角坐标系xoy中,已知椭圆C:
+
=1(a>b>0)的离心率为
,直线l:y=
与椭圆C相切.
(1)求椭圆C的方程;
(2)设AB是椭圆C上两个动点,点P(-1,
)满足
+
=λ
(0<λ<4且λ≠2),求直线AB的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)设AB是椭圆C上两个动点,点P(-1,
| 3 |
| 2 |
| PA |
| PB |
| PO |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由直线l:y=
与椭圆C相切,可得b,利用离心率为
,可得
=
,又a2-b2=c2=1,联立解得a2,b2即可;
(2)设直线y=kx+m,与椭圆方程联立可得根与系数的关系,再利用向量运算和向量相等即可得出.
| 3 |
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
(2)设直线y=kx+m,与椭圆方程联立可得根与系数的关系,再利用向量运算和向量相等即可得出.
解答:
解:(1)∵直线l:y=
与椭圆C相切,∴b=
,
∵离心率为
,∴
=
,
又a2-c2=b2=3,联立解得a2=4,b2=3.
∴椭圆C的方程为
+
=1;
(2)设直线y=kx+m,代入椭圆方程,化为(3+4k2)x2+8kmx+4m2-12=0,
∵直线AB与椭圆有两个不同的交点,∴△=64k2m2-4(3+4k2)(4m2-12)>0,化为3+4k2-m2>0.(*)
∴x1+x2=-
.
∵满足
+
=λ
(0<λ<4,且λ≠2),
∴x1+x2+2=λ,y1+y2-3=-
λ,
又y1+y2=kx1+m+kx2+m=k(x1+x2)+2m,
∴(k+
)(x1+x2)+2m=0,
∴(k+
)×(-
)+2m=0,
化为m(2k-1)=0,
若m=0,则直线AB经过原点,此时
+
=2
,λ=2,不符合题意,因此m≠0.
∴2k-1=0,解得k=
.
| 3 |
| 3 |
∵离心率为
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
又a2-c2=b2=3,联立解得a2=4,b2=3.
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线y=kx+m,代入椭圆方程,化为(3+4k2)x2+8kmx+4m2-12=0,
∵直线AB与椭圆有两个不同的交点,∴△=64k2m2-4(3+4k2)(4m2-12)>0,化为3+4k2-m2>0.(*)
∴x1+x2=-
| 8km |
| 3+4k2 |
∵满足
| PA |
| PB |
| PO |
∴x1+x2+2=λ,y1+y2-3=-
| 3 |
| 2 |
又y1+y2=kx1+m+kx2+m=k(x1+x2)+2m,
∴(k+
| 3 |
| 2 |
∴(k+
| 3 |
| 2 |
| 8km |
| 3+4k2 |
化为m(2k-1)=0,
若m=0,则直线AB经过原点,此时
| PA |
| PB |
| PO |
∴2k-1=0,解得k=
| 1 |
| 2 |
点评:本题中考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量的运算与相等等基础知识与基本技能方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=(x2-2x)ex,x∈[-2,+∞),f′(x)是函数f(x)的导函数,且f′(x)有两个零点x1和x2(x1<x2),则f(x)的最小值为( )
| A、f(x1) |
| B、f(x2) |
| C、f(-2) |
| D、以上都不对 |
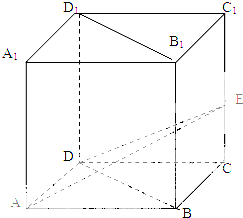 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为棱CC1的中点. 在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.
在△ABC中,AB=4,AC=3,M,N分别是AB,AC的中点.