题目内容
17. 在边长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.
在边长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点.(1)求证:CF∥平面A1DE;
(2)求直线AA1与平面A1DE所成角的余弦值.
分析 (1)取A1D中点M,连接FM,推导出平行四边形CFME,由此能证明CF∥平面A1DE.
(2)以D为坐标原点,DA、DC、DD1所在直线为轴建系,利用向量法能求出直线AA1与平面A1DE所成角的余弦值.
解答 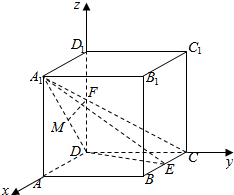 解:(1)取A1D中点M,连接FM,
解:(1)取A1D中点M,连接FM,
∵F为DD1中点,
∴FM∥A1D1且FM=$\frac{1}{2}$A1D1,…(3分)
又∵CE∥A1D1且$CE=\frac{1}{2}{A_1}{D_1}$,∴FM∥CE且FM=CE,
∴平行四边形CFME,∴CF∥ME,
又∵EM⊆面A1DE,∴CF∥平面A1DE.…(5分)
(2)以D为坐标原点,DA、DC、DD1所在直线为轴建系,
则A(1,0,0),A1(1,0,1),E($\frac{1}{2}$,1,0),…(6分)
∴$\overrightarrow{A{A}_{1}}$=(0,0,1),面A1DE的法向量可取$\vec u=(-1,\frac{1}{2},1)$,…(8分)
∴cos<$\overrightarrow{A{A}_{1}},\overrightarrow{μ}$>=$\frac{\overrightarrow{A{A}_{1}}•\overrightarrow{μ}}{|\overrightarrow{A{A}_{1}}|•|\overrightarrow{μ}|}$=$\frac{2}{3}$,…(9分)
∴cos$θ=sin<\overrightarrow{A{A}_{1}},\overrightarrow{μ}>$=$\frac{\sqrt{5}}{3}$.
∴直线AA1与平面A1DE所成角的余弦值为$\frac{\sqrt{5}}{3}$.…(10分)
点评 本题考查线面平行的证明,考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| A. | x+2y-3=0 | B. | 2x+y-3=0 | C. | 2x+y-1=0 | D. | 2x-y-1=0 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
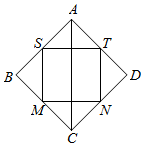 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )| A. | 8:1 | B. | 2:1 | C. | 4:3 | D. | 8:3 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |