题目内容
如果本金为a,每期利率为r,按复利计算,本利和为y,则存x期后,y与x之间的函数关系是 .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据按复利计算时,本利和y与存期x的函数关系是指数函数模型,写出它的函数关系式即可.
解答:
解:当本金为a,每期利率为r,按复利计算时,
本利和y与存期x的函数关系为
y=a(1+r)x.
故答案为:y=a(1+r)x.
本利和y与存期x的函数关系为
y=a(1+r)x.
故答案为:y=a(1+r)x.
点评:本题考查了指数函数模型的应用问题,是基础题目.

练习册系列答案
相关题目
函数y=
的定义域为( )
3x-
|
| A、[0,+∞) | ||
B、[
| ||
| C、[-1,+∞) | ||
| D、(-∞,-1] |
函数f(x)=x2-2lnx的单调减区间是( )
| A、(0,1) |
| B、(1,+∞) |
| C、(-∞,1) |
| D、(-1,1) |
若已知两个变量x 和y 之间具有线性相关系,4 次试验的观测数据如下:
经计算得回归方程
=bx+a系数b=0.7,则a等于( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| ∧ |
| y |
| A、0.34 | B、0.35 |
| C、0.45 | D、0.44 |
已知直三棱柱ABC-A1B1C1的六个顶点在球O上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的面积为( )
| A、153π | B、169π |
| C、10π | D、90π |
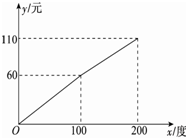 某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示.
某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示.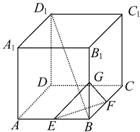 在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )
在棱长为1的正方体AC1中,E为AB的中点,点P为侧面BB1C1C内一动点(含边界),若动点P始终满足PE⊥BD1,则动点P的轨迹的长度为( )