题目内容
14、曲线y=2x3-3x2共有
2
个极值.分析:由题意可得:y′=6x2-6x=6x(x-1),令y′>0可得:x>1或x<0;令y′<0可得:0<x<1,再判断出函数的单调性,进而得到答案.
解答:解:由题意可得:y′=6x2-6x=6x(x-1),
令y′>0可得:x>1或x<0;令y′<0可得:0<x<1,
所以当x∈(-∞,0)时,y'>0,即函数在此区间内单调递增;
当x∈(0,1)时,y'<0,即函数在此区间内单调递减;
当x∈(1,+∞)时,y'>0,即函数在此区间内单调递增;
∴x=0与x=1分别为函数的极大值与极小值点.
故答案为:2.
令y′>0可得:x>1或x<0;令y′<0可得:0<x<1,
所以当x∈(-∞,0)时,y'>0,即函数在此区间内单调递增;
当x∈(0,1)时,y'<0,即函数在此区间内单调递减;
当x∈(1,+∞)时,y'>0,即函数在此区间内单调递增;
∴x=0与x=1分别为函数的极大值与极小值点.
故答案为:2.
点评:本题考查利用导熟研究函数的极值.可导函数的极值点一定是导数为0的根,但导数为0的点不一定是极值点,故需要验证.

练习册系列答案
相关题目
 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.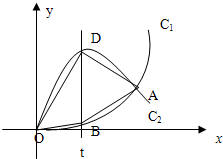 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=

 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.