题目内容
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于点O、A,直线x=t(0<t<1)与曲线C1、C2分别相交于点B、D,
(Ⅰ)写出四边形ABOD的面积S与t的函数关系S=f(t);
(Ⅱ)讨论f(t)的单调性,并求f(t)的最大值。
(Ⅰ)写出四边形ABOD的面积S与t的函数关系S=f(t);
(Ⅱ)讨论f(t)的单调性,并求f(t)的最大值。

解:(Ⅰ)由题意得交点O、A的坐标分别是(0,0),(1,1),
f(t)=S△ABD+S△OBD= |BD|·|1-0|=
|BD|·|1-0|= |BD|=
|BD|= (-3t3+3t),
(-3t3+3t),
即f(t)=- (t3-t),(0<t<1)。
(t3-t),(0<t<1)。
(Ⅱ)f'(t)=- t2+
t2+ ,令f'(t)=0,解得t=
,令f'(t)=0,解得t= ,
,
当0<t< 时,f'(t)>0,从而f(t)在区间(0,
时,f'(t)>0,从而f(t)在区间(0, )上是增函数;
)上是增函数;
当 <t<1时,f'(t)<0,从而f(t)在区间(
<t<1时,f'(t)<0,从而f(t)在区间( ,1)上是减函数;
,1)上是减函数;
所以当t= 时,f(t)有最大值为f(
时,f(t)有最大值为f( )=
)= 。
。
f(t)=S△ABD+S△OBD=
 |BD|·|1-0|=
|BD|·|1-0|= |BD|=
|BD|= (-3t3+3t),
(-3t3+3t),即f(t)=-
 (t3-t),(0<t<1)。
(t3-t),(0<t<1)。(Ⅱ)f'(t)=-
 t2+
t2+ ,令f'(t)=0,解得t=
,令f'(t)=0,解得t= ,
,当0<t<
 时,f'(t)>0,从而f(t)在区间(0,
时,f'(t)>0,从而f(t)在区间(0, )上是增函数;
)上是增函数;当
 <t<1时,f'(t)<0,从而f(t)在区间(
<t<1时,f'(t)<0,从而f(t)在区间( ,1)上是减函数;
,1)上是减函数;所以当t=
 时,f(t)有最大值为f(
时,f(t)有最大值为f( )=
)= 。
。 
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=t(0<t<1)与曲线C1,C2分别交于B,D.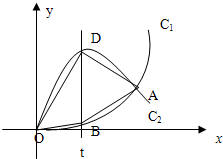 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x= (2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB.
(2007•广州一模)如图,已知曲线C1:y=x2与曲线C2:y=-x2+2ax(a>1)交于点O,A,直线x=t(0<t≤1)与曲线C1,C2分别相交于点D,B,连结OD,DA,AB,OB. (2009•黄冈模拟)如图,已知曲线
(2009•黄冈模拟)如图,已知曲线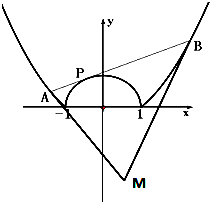 如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.
如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.