题目内容
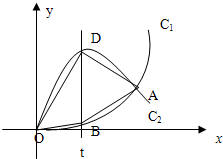如图，已知曲线C1：y=x3（x≥0）与曲线C2：y=-2x3+3x（x≥0）交于O，A，直线x=| 1 |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
分析：将四边形ABOD的面积S分割成两个小三角形的面积，通过求出交点坐标，可求面积
解答：解：（Ⅰ）由
得交点O．A的坐标分别是（0，0），（1，1）
同理可求得B(
，
)D(
，
)．
∴S△ABO+S△OBD=
|BD|•|1-0|=
．
故选A．
|
同理可求得B(
| 1 |
| 3 |
| 1 |
| 27 |
| 1 |
| 3 |
| 25 |
| 27 |
∴S△ABO+S△OBD=
| 1 |
| 2 |
| 4 |
| 9 |
故选A．
点评：方程的思想，是分析数学问题中变量间的等量关系，从而建立方程或方程组，通过解方程或方程组，或者运用方程的性质去分析、转化问题，使问题获得解决．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知曲线C1：y=x3（x≥0）与曲线C2：y=-2x3+3x（x≥0）交于O，A，直线x=t（0＜t＜1）与曲线C1，C2分别交于B，D．
（2007•广州一模）如图，已知曲线C1：y=x2与曲线C2：y=-x2+2ax（a＞1）交于点O，A，直线x=t（0＜t≤1）与曲线C1，C2分别相交于点D，B，连结OD，DA，AB，OB．
（2009•黄冈模拟）如图，已知曲线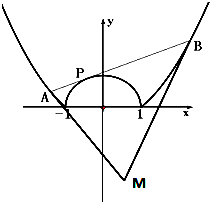
如图，已知曲线C1：x2+y2=1（|x|＜1），C2：x2=8y+1（|x|≥1），动直线l与C1相切，与C2相交于A，B两点，曲线C2在A，B处的切线相交于点M．