题目内容
椭圆C：
+
=1的焦距是 ．
| x2 |
| 25 |
| y2 |
| 9 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：直接从方程中解读出椭圆中基本参量的数值；然后通过椭圆中a、b、c之间的等量关系，即可解出c，进而得到2c，即该椭圆的焦距．
解答：
解：依题意得，a2=25，b2=9，
又∵在任意椭圆中有a2=b2+c2，从而c2=a2-b2=16（c＞0），解得c=4．
则该椭圆的焦距即2c=2×4=8，
故答案为：8．
又∵在任意椭圆中有a2=b2+c2，从而c2=a2-b2=16（c＞0），解得c=4．
则该椭圆的焦距即2c=2×4=8，
故答案为：8．
点评：本题考查了椭圆中各个参量的意义以及在方程中相应的相关表示，以及椭圆中重要的基本关系a2=b2+c2．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
若f（x）为R上的偶函数，g（x）=f（x-1）为R上的奇函数，且g（1）=2，则f（2014）的值为（ ）
| A、1 | B、2 | C、-1 | D、-2 |
在数列{an}中，a1=3，an+1=an+lg（1+
）（n∈N*），则an=（ ）
| 1 |
| n |
| A、lgn | ||||||
B、3+lg（
| ||||||
| C、3+lgn | ||||||
| D、3+3lng |
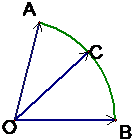给定两个长度为1的平面向量