题目内容
17．已知△ABC的面积为$\frac{16}{3}$$\sqrt{3}$，BC=6，∠A=60°，求△ABC的周长．分析 由余弦定理可得：62=b2+c2-2bccos60°，化为（b+c）2-3bc=36，又$\frac{1}{2}$bcsin60°=$\frac{16}{3}\sqrt{3}$，化为bc=$\frac{64}{3}$，联立解出即可得出．
解答 解：由余弦定理可得：62=b2+c2-2bccos60°，化为b2+c2-bc=36，
又$\frac{1}{2}$bcsin60°=$\frac{16}{3}\sqrt{3}$，化为bc=$\frac{64}{3}$，
∴（b+c）2-3bc=36，即（b+c）2=100，解得b+c=10．
∴a+b+c=16．
∴△ABC的周长是16．
点评 本题考查了余弦定理、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
△ABC中，AB=5，AC=12，BC=13，P为△ABC平面外一点，PA=PB=PC=7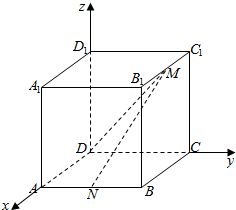
在长方体ABCD-A1B1C1D1中，|AB|=|BC|=2，|D1D|=3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系．