题目内容
17.已知直线kx-y+2k-1=0(k∈R)恒过圆C的圆心,且圆C的半径为2,则圆C的方程是(x+2)2+(y+1)2=4.分析 由题意直线kx-y+2k-1=0(k∈R)恒过定点(-2,-1)即圆心,即可写出圆的方程.
解答 解:由题意直线kx-y+2k-1=0(k∈R)恒过定点(-2,-1)即圆心,
∵圆C的半径为2,
∴圆C的方程是(x+2)2+(y+1)2=4,
故答案为(x+2)2+(y+1)2=4.
点评 本题考查圆的方程,考查直线过定点,考查学生的计算能力,比较基础.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
7.为了解重庆某社区居民的家庭年收入和年支出的关系,随机调查了5户家庭,得到统计数据表,根据表中可得回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=0.5,据此估计,该社区一户收入为16万元家庭年支出为( )
| 收入x(万元) | 6 | 8 | 10 | 12 | 14 |
| 支出y(万元) | 6 | 7 | 8 | 9 | 10 |
| A. | 15万元 | B. | 14万元 | C. | 11万元 | D. | 10万元 |
8.如图四个散点图中,适合用线性回归模型拟合其中两个变量的是( )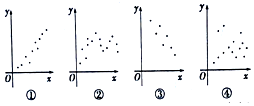

| A. | ①② | B. | ①③ | C. | ②③ | D. | ③④ |
12.若i是虚数单位,复数$\frac{1-2i}{i}$的虚部为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
 体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π].
体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上,球心O在此三棱锥内部,且R:BC=2:3,点E为线段BD上一点,且DE=2EB,过点E作球O的截面,则所得截面圆面积的取值范围是[8π,16π]. 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB=2,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.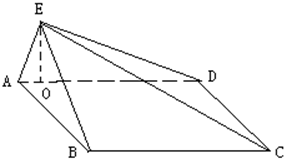 如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.
如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.