题目内容
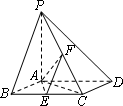
如下图,已知四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=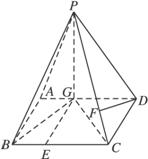
(1)求点D到平面PBG的距离;
(2)若F点是棱PC上一点,且DF⊥GC,求![]() 的值.
的值.
解析:(1)VP-BCG=![]() ·PG·
·PG·![]() BG·GC=
BG·GC=![]() ,
,
即![]() PG·2×2=8
PG·2×2=8![]() PG=4.
PG=4.
VD-PBG=VP-BDG=![]() S△ABD·PG·
S△ABD·PG·![]() =23VP-BCG=
=23VP-BCG=![]() ,
,
即![]() h·
h·![]() BG·PG=
BG·PG=![]() ,∴h=
,∴h=![]() .
.
即点D到平面PBG的距离为![]() .
.
(2)以GB,GC,GP为x,y,z轴建系,
则G(0,0,0)、B(2,0,0)、C(0,2,0),
D(-![]() ,
,![]() ,0),P(0,0,4),
,0),P(0,0,4),
设![]() =λ,则F(0,
=λ,则F(0, ).
).
∴![]() =(
=(![]() ),
),![]() =(0,2,0).
=(0,2,0).
由DF⊥GC得![]() ·
·![]() =2(
=2(![]() )=0,
)=0,
∴λ=2,即![]() =2.
=2.

练习册系列答案
相关题目
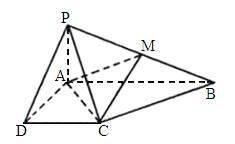
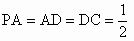 ,AB=1,M是PB的中点.
,AB=1,M是PB的中点.
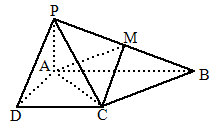
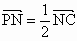 ,PM=MD.
,PM=MD.
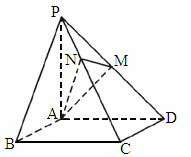
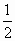 AB=1,M是PB的中点.
AB=1,M是PB的中点.