题目内容
(2007
成都模拟)如下图,已知四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在棱PD、PC上,且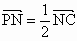 ,PM=MD.
,PM=MD.
(1)
求证:PC⊥AM;(2)
求证:PC⊥平面AMN;(3)
求二面角B—AN—M的大小.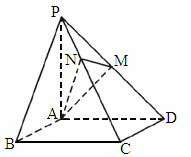
答案:略
解析:
解析:
|
解析: (1)因为四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,故建立如图所示的空间直角坐标系A-xyz,又PA=AD=2,则有P(0,0,2),D(0,2,0),M(0,1,1),C(2,2,0).∴ 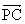 =(2,2,-2), =(2,2,-2), =(0,1,1). =(0,1,1).
∵ 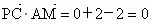 ,∴PC⊥AM. ,∴PC⊥AM.
(2) 设N(x,y,z),∵ ,则有 ,则有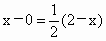 ,∴ ,∴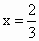 .同理可得 .同理可得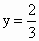 , ,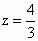 .即 .即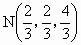 . .
由 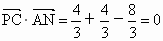 , ,
∴ PC⊥AN.又∵PC⊥AM,AM∩AN=A,∴ PC⊥平面AMN.
(3) 连接BN,设平面BAN的法向量为n=(x,y,z),由 取 n=(0,-2,1).
∴ 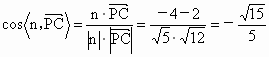 . .
结合图形可知,所求二面角 B-AN-M的大小为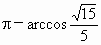 . . |

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
(2007
成都模拟)已知无穷等比数列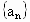 的公比为
的公比为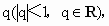
 为其前n项和
为其前n项和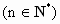 ,又
,又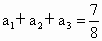 ,
,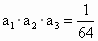 ,则
,则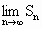 的值为
的值为
[
]|
A .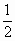 |
B .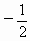 |
C .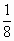 |
D .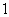 |


 =(2
=(2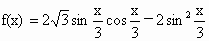 .
.
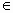 [0,π],求函数f(x)的值域;
[0,π],求函数f(x)的值域;
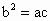 ,求sinA的值.
,求sinA的值. (其中e=2.71828…是自然对数的底数);
(其中e=2.71828…是自然对数的底数);
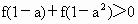 ,则实数a的取值范围为__________.
,则实数a的取值范围为__________.