题目内容
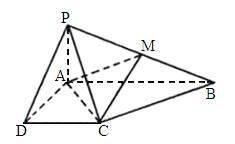
如下图,已知四棱锥
P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且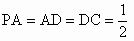 ,AB=1,M是PB的中点.
,AB=1,M是PB的中点.
(1)
证明:面PAD⊥面PCD;(2)
求AC与PB所成的角的余弦值.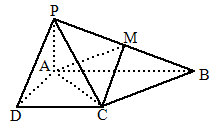
答案:略
解析:
解析:
|
证明:以 A为坐标原点,AD长为单位长度,如下图建立空间直角坐标系,
则各点坐标为 A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1), . .
(1) 因为由题设知 AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.又DC在面PCD上,故面PAD⊥面PCD.(2) 因 , , , ,
故  , ,
所以  . . |

练习册系列答案
相关题目

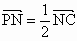 ,PM=MD.
,PM=MD.
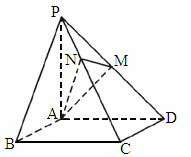
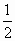 AB=1,M是PB的中点.
AB=1,M是PB的中点.