题目内容
(
南昌四校模拟)如下图,已知四棱锥P—ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=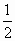 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)
证明:面PAD⊥面PCD;(2)
求AC与PB所成的角;(3)
求面AMC与面BMC所成二面角的大小.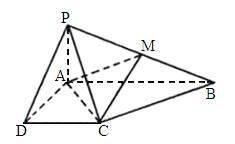
答案:略
解析:
解析:
|
解析:解法一: (1)∵PA⊥面ABCD,CD⊥AD,∴由三垂线定理得CD⊥PD. (1分)
因而, CD与面PAD内两条相交直线AD,PD都垂直,∴ CD⊥面PAD. (2分)又 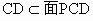 ,∴面PAD⊥面PCD. (3分) ,∴面PAD⊥面PCD. (3分)
(2) 过点B作BE∥CA,且BE=CA,则∠PBF是AC与PB所成的角 (4分)连结 AE,可知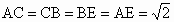 .又AB=2, .又AB=2,
所以四边形ACBE为正方形. (5分) 由 PA⊥面ABCD得∠PBF=90°,在 Rt△PEB中,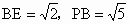 , ,
∴  , ,
∴ AC与PB所成的角为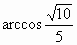 . (7分) . (7分)
(3) 作AN⊥CM,垂足为N,连结BN,在 Rt△PAB中,AM=MB,又AC=CB,∴△ AMC≌△BMC,∴BN⊥CM,故∠ ANB为所求二面角的平面角.∵ CB⊥AC,由三垂线定理,得CB⊥PC.在 Rt△PCB中,CM=MB,所以 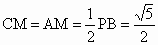 . .
在等腰三角形 AMC中,
∴ 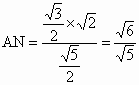 . (10分) . (10分)
又 AB=2,∴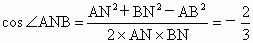 , ,
故所求的二面角为 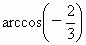 . (12分) . (12分)
解法二:因为 PA⊥AD,PA⊥AB,AD⊥AB,以A为坐标原点建立如图所示空间直角坐标系,则各点坐标为A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M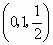 . (1分) . (1分)
(1) 因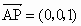 , ,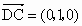 , ,
故  ,所以AP⊥DC. ,所以AP⊥DC.
由题设知 AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得 DC⊥面PAD,又DC在面PAD上,故面 PAD⊥面PCD. (3分)(2) 因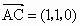 , ,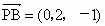 , ,
故 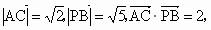
所以 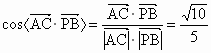 . .
∴ AC与PB所成的角为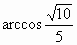 . (7分) . (7分)
(3) 在MC上取一点N(x,y,z),使 AN⊥MC,设 ,其中 ,其中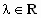 , ,
∵ 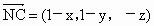 , ,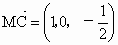 , ,
∴ x=1-λ,y=1,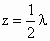 . .
∵ AN⊥MC,∴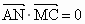 , ,
即 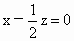 , ,
即 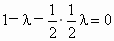 ,解得 ,解得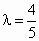 . (8分) . (8分)
所以点 N的坐标为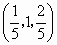 , ,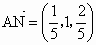 , ,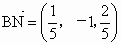 , ,
∴ 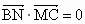 ,∴BN⊥MC. ,∴BN⊥MC.
所以∠ ANB为所求二面角的平面角. (10分)∵  , ,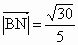 , ,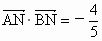 , ,
∴ 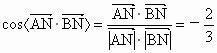 , ,
故所求的二面角为 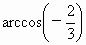 . . |

练习册系列答案
相关题目



 -
-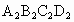 的棱长为a,A、B、C、D分别在
的棱长为a,A、B、C、D分别在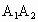 、
、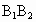 、
、 、
、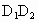 上,且
上,且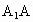 =
=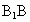 =
=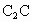 =
=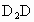 =
=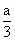 ,则四边形ABCD的面积为
,则四边形ABCD的面积为
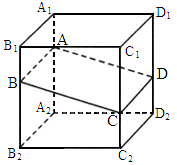
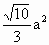
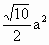
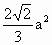
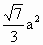

 中,点E为棱
中,点E为棱 的动点.
的动点.
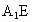 ⊥BD;
⊥BD;
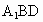 ⊥平面EBD;
⊥平面EBD;
 —BD—E的大小为45°?如果存在,试确定点E在棱
—BD—E的大小为45°?如果存在,试确定点E在棱 上的位置;如果不存在,请说明理由.
上的位置;如果不存在,请说明理由.

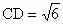 .
.
