题目内容
已知P为△ABC所在平面外一点,G1、G2、G3分别是△PAB、△PCB、△PAC的重心.
(1)求证:平面G1G2G3∥平面ABC;
(2)求S△ ∶S△ABC.
∶S△ABC.
(1)求证:平面G1G2G3∥平面ABC;
(2)求S△
 ∶S△ABC.
∶S△ABC.(1)证明略(2)S△ ∶S△ABC=1∶9
∶S△ABC=1∶9
 ∶S△ABC=1∶9
∶S△ABC=1∶9(1) 如图所示,连接PG1、PG2、PG3并延长分别与边AB、BC、AC交于点D、E、F,连接DE、EF、FD,则有PG1∶PD=2∶3,

PG2∶PE=2∶3,∴G1G2∥DE.
又G1G2不在平面ABC内,
∴G1G2∥平面ABC.同理G2G3∥平面ABC.
又因为G1G2∩G2G3=G2,
∴平面G1G2G3∥平面ABC.
(2) 由(1)知 =
= ,∴G1G2=
,∴G1G2= DE.
DE.
又DE= AC,∴G1G2=
AC,∴G1G2= AC.
AC.
同理G2G3= AB,G1G3=
AB,G1G3= BC.
BC.
∴△G1G2G3∽△CAB,其相似比为1∶3,
∴S△ ∶S△ABC=1∶9.
∶S△ABC=1∶9.

PG2∶PE=2∶3,∴G1G2∥DE.
又G1G2不在平面ABC内,
∴G1G2∥平面ABC.同理G2G3∥平面ABC.
又因为G1G2∩G2G3=G2,
∴平面G1G2G3∥平面ABC.
(2) 由(1)知
 =
= ,∴G1G2=
,∴G1G2= DE.
DE.又DE=
 AC,∴G1G2=
AC,∴G1G2= AC.
AC.同理G2G3=
 AB,G1G3=
AB,G1G3= BC.
BC.∴△G1G2G3∽△CAB,其相似比为1∶3,
∴S△
 ∶S△ABC=1∶9.
∶S△ABC=1∶9.
练习册系列答案
相关题目
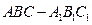 中,
中,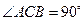 ,
,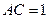 ,
,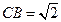 ,侧棱
,侧棱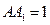 ,侧面
,侧面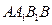 的两条对角线交点为
的两条对角线交点为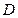 ,
,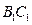 的中点为
的中点为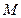 .
.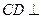 平面
平面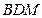 .
.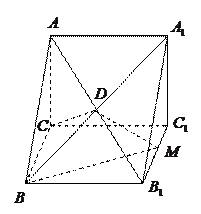
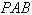 是否垂直于平面
是否垂直于平面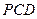 ?
?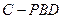 的体积.
的体积.

 CC1.
CC1.