题目内容
如图,在三棱柱ABCA′B′C′中,点E、F、H、K分别为AC′、CB′、A′B、B′C′的中点,G为△ABC的重心,从K、H、G、B′中取一点作为P,使得该棱柱恰有2条棱与平面PEF平行,则P为( )
A.K B.H C.G D.B′
A.K B.H C.G D.B′
C
若P为K点,则棱柱中A′B′、AA′、BB′、CC′等均与平面PEF平行,不合题意.
若P为H点,则棱柱中B′C′、A′B′、A′C′、AB、BC、AC均与平面PEF平行,也不合题意.
若P为B′点,则棱柱中无棱与平面PEF平行,只有当P为G点时,棱柱中恰有2条棱AB、A′B′与平面PEF平行.
若P为H点,则棱柱中B′C′、A′B′、A′C′、AB、BC、AC均与平面PEF平行,也不合题意.
若P为B′点,则棱柱中无棱与平面PEF平行,只有当P为G点时,棱柱中恰有2条棱AB、A′B′与平面PEF平行.
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
中，E、F、G、H、M、N分别是正方体六个面的中心．求证：平面EFG//平面HMN.
中，
分别是
的中点．
平面
；（2）
平面
．
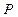
（2）若F为侧棱PA上的一点，且
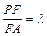， 则为何值时，PA平面BDF？ 并求此时几何体F—BDC的体积．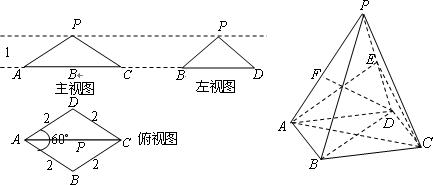
.
∶S△ABC.
，
平面
，且
，
，
．
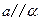