题目内容
(12分)如图,菱形 的边长为4,
的边长为4, ,
, .将菱形
.将菱形 沿
沿
对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.

(1)求证:OM∥平面ABD;
(2)求证:平面DOM⊥平面ABC
(3)求三棱锥B﹣DOM的体积.
(1)见解析;(2)见解析;(3)
【解析】
试题分析:(1)∵O为AC的中点,M为BC的中点,∴OM∥AB.
又∵OM?平面ABD,AB?平面ABD,∴OM∥平面ABD.
(2)∵在菱形ABCD中,OD⊥AC,∴在三棱锥B-ACD中,OD⊥AC.
在菱形ABCD中,AB=AD=4,∠BAD=60°,可得BD=4.
∵O为BD的中点,∴DO= ,BD=2.∵O为AC的中点,M为BC的中点,∴OM=
,BD=2.∵O为AC的中点,M为BC的中点,∴OM= ,AB=2.
,AB=2.
因此, ,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,
,可得OD⊥OM.∵AC、OM是平面ABC内的相交直线,
∴OD⊥平面ABC. ∵OD?平面DOM,∴平面DOM⊥平面ABC.
(3)由(2)得,OD⊥平面BOM,所以OD是三棱锥D-BOM的高.
由OD=2, ,
,
所以 .
.
考点:本题考查线面平行的判定,面面垂直的判定,求三棱锥的体积

练习册系列答案
相关题目
 :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。 ,C
,C 的普通方程;
的普通方程; 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (t为参数)距离的最小值及此时Q点坐标.
(t为参数)距离的最小值及此时Q点坐标.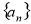 中,前n项和为
中,前n项和为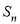 ,已知
,已知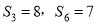 ,则
,则 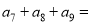 ( )
( )  B.
B. C.
C. D.
D.
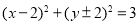
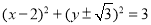
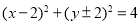
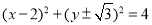
 ,直线
,直线 (
( 为参数)
为参数) 的参数方程,直线
的参数方程,直线 的普通方程;
的普通方程; 作与
作与 ,求
,求 的最大值与最小值.
的最大值与最小值. 中,
中, ,
, ,点
,点 是斜边
是斜边 上的
上的 _________.
_________. ,
, 满足约束条件
满足约束条件 ,则
,则 的最大值等于 ( )
的最大值等于 ( ) 均为常数
均为常数 ,当
,当 时取极大值,当
时取极大值,当 时取极小值,则
时取极小值,则 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 与
与 的夹角是
的夹角是 ,且
,且 ,
, ,若
,若 ,则实数
,则实数 _______.
_______.